تحلیل شبکه های اجتماعی به صورت خلاصه و کاربردی
عناوين مطالب: '
- مقدمه ای بر تحلیل شبکه های اجتماعی:
- 1- مرکزیت یا (centrality) در تحلیل شبکه های اجتماعی:
- 2- خوشه بندی گراف شبکه های اجتماعی یا تشخیص انجمن ها
- 3- الگوریتم های بصری سازی تحلیل شبکه های اجتماعی
- 4- الگوریتم های پیشبینی ارتباطات در تحلیل شبکه های اجتماعی
- ۵- الگوریتم های نمومه برداری گراف در تحلیل شبکه های اجتماعی
- ۶- تحلیل انتشار در تحلیل شبکه های اجتماعی
مقدمه ای بر تحلیل شبکه های اجتماعی:
شبکههای اجتماعی یا به عبارتی رسانه های اجتماعی با دادههای مربوط به انسانها که معمولا توسط ایشان تولید میشوند و اغلب در برگیرنده ویژگی های اجتماعی آنها هستند توسعه پیدا میکنند. تحلیل شبکه های اجتماعی (Social Network Analysis) که گاهی به اختصار به آن SNA و گاهی هم شبکه های پیچیده پویا گفته میشود، به معنای فرایند بررسی و ارزیابی ساختارهای یک گراف از تعامل انسانهاست که با خطوط ارتباطی به یکدیگر متصل هستند. در حقیقت تحلیل شبکههای اجتماعی فرآیند تحقیق و بررسی ساختارهای اجتماعی با استفاده از نظریه شبکه و نظریه گراف است. (برای پیش نیاز این مطلب، مبحث مربوط به تئوری گراف را حتما مطالعه کنید)
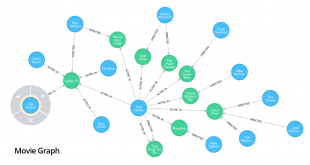
به عنوان مثالی از تحلیل شبکههای اجتماعی میتوان به بررسی الگوهای موجود در گراف شبکه اشاره کرد که براساس آن میتوان به دانش الگوهای رفتاری انسانها و در نتیجه اطلاعات ارزشمند قابل تحلیل و کاوش درباره روش تعاملات بشر دست پیدا کرد. نتایج حاصل از تحلیل شبکههای اجتماعی در برگیرنده ارزش و قدرتی است که توسط بسیاری از سازمانها و بنگاه های (کوچک، متوسط و بزرگ) دولتی و خصوصی برای بیشینهسازی بازده مورد استفاده قرار میگیرد. و گاهی هم به عنوان یکی از مولفه های جنگ شناختی مورد استفاده قرار میگیرد. تصویر زیر گراف ارتباطی توئیتر باراک اوباما را نمایش می دهد.

شبکههاي اجتماعي به طور عمده از دو ديدگاه قابل بررسي و تحلیل ميباشند:
1- تحلیل ساختار (یا تحلیل استاتیک) که بررسی ساختار و توپولوژی گراف شبکه های اجتماعی
2- تحلیل ديناميک (به زبان ساده داینامیک یعنی بررسی در بستر زمان یا تحلیل در بردار زمان).
گرافها به عنوان ساختارهای ریاضی که روابط اشیا با هم را در سطح انتزاع مناسبی نشان میدهند به طور گسترده در مدلسازی مسائل مختلف مورد استفاده قرار گرفتهاند. به همین سبب، در اختیار داشتن روش ها و ابزارهایی مناسب برای تحلیل آنها به یک ضرورت مبدل شده است. بررسيها نشان ميدهد که اين شبکه ها در خصوصيات مشترک ساختاري به طرز قابل توجّهي اشتراک دارند. تحلیل های با ارزشی به منظور گراف کاوی تا کنون ارائه شده است. ولی معمولا شش دسته الگوریتم زیر بیشترین کاربردرا در تحلیل شبکه های اجتماعی دارند.
1- الگوریتم های تشخیص مرکزیت
2- الگوریتم های تشخیص انجمن
3- الگوریتم های بصری سازی
4- الگوریتم های پیشبینی ارتباطات یا لینک
5- الگوریتم های نمومه برداری
6- تحلیل انتشار
در ادامه یکی از این 6 دسته را معرفی می کنیم:
1- مرکزیت یا (centrality) در تحلیل شبکه های اجتماعی:
نحوه اتصال یک نود به نودهای دیگر در یک شبکه اجتماعی میتواند اطلاعاتی راجع به مهم بودن و یا مهم نبودن آن نود در کاربردهای خاص مشخص نماید. بعنوان مثال میتوانیم مشخص کنیم کدام نود در انتشار شایعه بیشترین تاثیر را در یک شبکه اجتماعی دارد. برای سنجش میزان اهمیت، از شاخصهای کمّی استفاده میشود که معیارهای مرکزیت نام دارند. محاسبه این معیارها معمولا روی شبکه های بزرگ طولانی و وقت گیر است و به همین دلیل تحقیقات گسترده ای در دنیا صورت گرفته تا الگوریتمهایی کشف شوند که میزان این محاسبات را تا حد ممکن کاهش دهند و یا اینکه محاسبات را به صورت موازی و توزیع شده بر روی کامپیوترهای مختلف انجام دهند. از مهم ترین معیار های مرکزیت میتوان به موارد زیر اشاره کرد.
- فراوانی درجات گره ها(Degree distribute)
- بینابینی (betweenness)
- نزدیکی (closeness)
- دوری از مرکز(Eccentricity)
- آسیب پذیری (Vulnerability)
- دسترسی گره ها(Reach)
- کارایی گره(Efficiency)
- تنش(Stress)
- قدرت(Power)
- بردار ویژه(Eigen Vector)
- آسیب پذیری گره(Node vulnerability)
- رتبه صفحه(Page rank)
- Hits
یک دسته بندی مناسب بین روش های مختلف تشخیص مرکزیت می تواند به صورت زیر باشد:
روشهای مبتنی بر همسایه مانند:
- مرکزیت درجه
- امتیازدهی K-Shell
روشهای مبتنی بر مسیر مانند:
- مرکزیت نزدیکی..
- مرکزیت بینابینی..
- حفره ساختاری..
روشهای تکراری یا مبتنی بر ارزش مانند:
- مرکزیت مقادیر ویژه
- PageRank
برای مطالعه بیشتر در این زمینه به مبحث معیارهای مرکزیت (Centrality) در تحلیل شبکه های اجتماعی مراجعه کنید.
2- خوشه بندی گراف شبکه های اجتماعی یا تشخیص انجمن ها
خوشه بندی گراف (Clustering) شبکه های اجتماعی در جهت تشخیص انجمن هایی (community detection) از انسان های به هم مرتبط انجام میشود. یکی از تحلیلهای مهمی که روی گرافها انجام میشود خوشه بندی نودهای گراف است. خوشه بندی نودها در گراف در حقیقت همان مساله تشخیص انجمنهای گراف است. یکی از کاربردیترین مسائل در علم کامپیوتر و هوش مصنوعی، مسئلهی خوشهبندی (Clustering) دادهها است. مسئله خوشهبندی گرافها از مسائل مهم در بسیاری از زمینهها مانند شبکههای اجتماعی، بیوانفورماتیک و الکترونیک می باشد. لذا محققان زیادی از رشتههای مختلف تحقیقات متنوعی را پیرامون آن انجام دادهاند.از طرفی امکان مدلسازی (Modeling) بسیاری از مسائل با نظریه گراف و نیاز به تحلیل این گرافها موجب شده است تا توجه گستردهای به خوشهبندی گرافها شده و روشهای متعددی برای آن ارائه شود.
هدف از خوشهبندی، استخراج بخشهایی از دادهها است که شباهت زیادی با هم دارند. به زبان دیگر، در خوشهبندی، دادهها را به نحوی در گروههایی تقسیم میکنیم که دادههای مربوط به هر گروه ویژگیهای نزدیک به هم داشته باشند و دادههای موجود در دو گروه مختلف، ویژگیهایی با اختلاف زیاد داشته باشند. به عنوان مثال، اگر ویژگیهای سیاسی افراد را در نظر بگیریم (فارغ از این که ارتباطات اجتماعی آنها چگونه است)، نتایج خوشهبندی در حالت ایدهآل افراد را به مجموعههایی تقسیم خواهد کرد که هر کدام گرایشهای سیاسی نزدیک به هم دارند و همچنین افراد گروههای متفاوت شباهت کمتری در نگرش سیاسی با هم دارند. روشهای خوشهبندی در کاربردهای مختلفی از جمله سادهسازی دادهها، تحلیل دادهها، شباهتسنجی دادهها و یافتن الگوها کاربرد دارند.
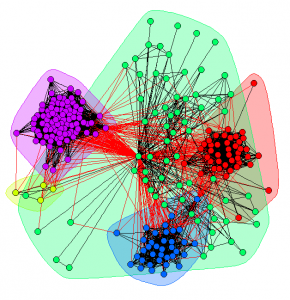
اهمیت خوشهبندی
با توجه به اهمیت خوشهبندی در تحلیل دادهها و گستردگی استفاده از گراف در مدلسازی مسائل، خوشهبندی گرافها به طور خاصی مورد توجه محققان قرار گرفته و روشهای مختلفی برای آن ارائه شده است. از آنجایی که محققان رشتههای مختلفی بر روی این مسئله کار کردهاند، رویکردهای متفاوتی نسبت به آن وجود دارد. ولی کلیت بیشتر این روشها پیدا کردن زیرگرافهایی است که ارتباط درونی زیاد و ارتباطات بیرونی کمی دارند.
به این دلیل که مفهوم جامع و مانعی از “ارتباط درونی زیاد” و “ارتباط بیرونی کم” وجود ندارد، در هر روش تعریفی خاصی از این موضوع شده است و بر اساس آن راهحلی برای آن ارائه شده است. به تعبیر دیگر میتوان گفت که خوشهبندی یک مسئله بهینهسازی است که به عنوان تابع هزینه (یا تابع هدف) آن، تعاریف متفاوتی ارائه شده است. به عنوان مثال، برخی از روشها بر مبنای الگوریتم حداکثر شار-حداقل برش سعی میکنند خوشهها را طوری پیدا کنند که شار عبوری از محل برش بیشینه شود. از طرفی برخی دیگر سعی میکنند با بیشینه کردن معیار پیمانگی (Modularity) خوشههای گراف را پیدا کنند.
دسته بندی الگوریتم های خوشه بندی
الگوریتمهای خوشه بندی به خودی خود و به صورت مستقیم قابل اعمال به مساله تشخیص انجمن در گراف نیستند. باید تبدیلاتی در این مرد صورت گیرد. از طرف دیگر اندازهی بسیار بزرگ گرافهای مورد بررسی در زمینهی شبکههای اجتماعی و بیوانفورماتیک، محققین این حوزهها را به سمت توسعه الگوریتمهایی که سربار محاسباتی پایینی داشته و قابلیت مقیاسپذیری بالایی دارند سوق داده است.
زیر به عناوین مهمترین روش ها و الگوریتم های خوشه بندی در گراف اشاره شده است.
روشهای خوشهبندی مبتنی بر فاصله
- روش K-Means
- روش K-Medoids.
- روش PAM
- روشCLARA
- روش OPTICS
روشهای خوشهبندی سلسله مراتبی
- Single Linkage.
- Complete Linkage.
- Average Linkage.
روشهای خوشهبندی گراف مبتنی بر پیمانگی یا ماژولاریتی (Modularity)
- روش گیروان و نیومن
- روش تیلور
- روش نیومن.
- روش Louvain
برای مطالعه بیشتر در این زمینه به مبحث خوشه بندی شبکه های اجتماعی مراجعه کنید.
3- الگوریتم های بصری سازی تحلیل شبکه های اجتماعی
بصری سازی گراف یا بازنمایی روشی به منظور قابل درک کردن گراف برای ذهن انسان است. نمایش بصری گراف برای استخراج اطلاعات و تحلیل گراف توسط انسان بسیار حائز اهمیت است. در حقیقت بخش نمایش بصری، وظیفه خلاصه سازی اطلاعات را نیز بعهده دارد. فیلد بصری سازی با فیلدهایی همچون علوم کامپیوتر و ریاضی، روانشناسی، رسانه، طراحی گرافیکی، هنر و کارتوگرافی رابطه مستقیم دارد. مسائل بازنمایی گراف معمولا NP-complete هستند و برای گرافهای بزرگ، قابل حل در زمان کم نمیباشند. در نتیجه مشکل اصلی الگوریتمهای بازنمایی گراف در مقیاس پذیری آنها است.
مشکلات بازنمایی گرافها
با بزرگ شدن گرافها مشکل اندازه صفحه و تعداد پیکسلها نیز به این امر اضافه میشود و نمیتوان حجم عظیمی از گراف را با نقاط کمی نشان داد. استفاده صحیح از اندازه نودها، پهنای یالها و رنگ و شفافیت آنها نیز خود مساله مهمی است. این که چه ویژگیهایی از نودها و یالها به صورت بصری با این تغییرات نمایش داده شود در درک بهتر گراف توسط انسان کمک خواهند کرد.
یکی دیگر از مشکلات بازنمایی بصری گرافها، خاص منظوره بودن تکنیکهای بازنمایی در عین متنوع بودن این تکنیکها است و همین باعث میشود اعمال هر تکنیک به دامنههای دیگر با محدویتهایی همراه باشد و یا کارکرد مطلوب را نداشته باشد. بعنوان مثال برخی تکنیکهای بازنمایی بصری روی درختها خوب کار میکنند. این الگوریتمها برای گرافهای شبکه اجتماعی که ساختار درختی ندارند مناسب نمیباشند. بهمین دلیل تمرکز ما بر روی این نوع الگوریتمها نخواهد بود.
ابزارهای بصری سازی شبکه های اجتماعی
بصری سازی گراف، ممکن است با تمرکز بر روی نود خاصی به عنوان کانون توجه صورت پذیرد. در این صورت آن را نمایش چشم ماهی (Fish eye visualization) گفته میشود. در نمایش هایی که کل شبکه در کنار هم رسم میشود سعی میشود نودهای مرتبط با هم کنار هم رسم شده و نودهای غیرمرتبط دور از هم در صفحه قرار گیرند تا کاربر مشاهده کننده دید مناسبی از کلیات شبکه داشته باشد. ابزارهای متنوعی از جمله نرم افزار پرکاربرد گفی (Gephi) و سایتو اسکیپ و انواع کامپوننت های جاوا اسکریپتی گراف به منظور بصری سازی و نمایش گراف تولید شده است.
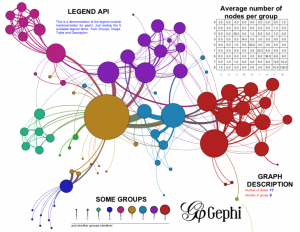
بصری سازی انجمنها
در مساله تشخیص انجمنها تلاش میشود نودهایی که با هم ارتباط زیادی دارند در یک انجمن و نودهایی که با هم ارتباط کمی دارند در انجمنهای مجزا قرار گیرند. الگوریتمهای بازنمایی گراف مشابه روشهای تشخیص انجمن تلاش میکنند تصویری دو بعدی یا سه بعدی از گراف ارائه کنند که در آن نودهایی که با هم ارتباط دارند در یک ناحیه و نقاطی که با هم ارتباط ندارند در نواحی دور از هم قرار گیرند. اگر چه همه روشها قصد دارند انجمنها را به نحو بهتری مشخص کنند اما ماهیتا با هم متفاوتند. الگوریتمهای بازنمایی سعی میکنند نمایش بصری را بهتر کنند و الگوریتمهای تشخیص انجمن از روی ساختار گراف این انجمنها را تشخیص میدهند و کاری به نمایش بصری آن ندارند. حتی انجمن های به هم مرتبط باید در بصری سازی به هم نزدیک باشند.
در نمایش کامل شبکه و بصری سازی گراف، معمولا فرض میشود میان نودهای مرتبط نیروهای جاذبه ای وجود دارند که همانند نیرویی که کرات را در کنار هم نگه میدارد، نودها را به هم نزدیک میکند. در مقابل میان نودهای غیرمرتبط نیروی دافعه ای فرض میشود که باعث دور شدن آنها از هم میگردد. در نتیجه مساله رسم گراف به یک مساله فیزیکی مبدل میشود که حل آن بسیار پیچیده است اما الگوریتمهای شهودی زیادی وجود دارند که بتوانند برای تعداد نود نسبتا کم این محاسبات را ساده کرده و در زمان معقول به انجام برسانند. این الگوریتم ها را الگوریتم های هدایت شونده با نیرو (force directed) می نامند.
انواع متنوعی از روش ها و الگوریتم های بصری سازی گراف یا بازنمایی در حوزه تحلیل شبکه های اجتماعی ارائه شده است که عناوین برخی از مهمترین آنها در ذیل آمده است که در آینده به بررسی آنها میپردازیم. این روش ها و الگوریتم ها در ابزار گراف کاوی محبوب گفی (Gephi) که در مبحث قبل به آن اشاره شد قابل استفاده است.
- Reingold Fruchterman-Reingold(FR)
- Force Atlas (FA)
- Yifan-Hu (YH)
- OpenOrd (OO)
نرم افزارهای بازنمایی گراف
بازنمایی مناسب باعث افزایش توان انسان برای پیداکردن ویژگیها در ساختار و دادههای گراف میشوند. با این حال، اجرای این فرآیند از نظر محاسباتی پیچیده بوده و به روشهای تخمینی و ساده سازی نیاز دارد. ابزارهای بازنمایی شبکه، علاوه بر دقت کافی و جذابیت بصری، لازم است به سوی بازنمایی سریع و بلادرنگ حرکت کنند تا امکان مشاهده آنی گراف را فراهم آورند. ابزارهای بازنمایی باید دارای کیفیت بصری بالا و قابل ترکیب با ویژگیهایی نظیر فیلترکردن دادههای غیر مهم، خوشهبندی نودها برای خلاصه کردن گراف و انجام تحلیلهای آماری باشند.
نرم افزارهای بازنمایی باید گراف را به گونهای رسم کنند که قواعد زیر در آنها رعایت شده باشد:
- نودها به صورت یکنواخت توزیع شوند و تا حد امکان همپوشانی با یکدیگر نداشته باشند.
- یالها تا حد ممکن مستقیم رسم شوند و کمتر همدیگر را قطع کنند.
- زیرگرافهای همریخت، در کل گراف به صورت یکسانی نشان داده شوند.
- نودهای مرتبط تا حد امکان کنار همدیگر رسم شوند.
- نودهای غیرمرتبط دور از هم رسم شوند.
- اجرای الگوریتم با دادههای یکسان نتایج یکسانی داشته باشد.
برای مطالعه بیشتر در این زمینه به مبحث بصری سازی گراف مراجعه کنید.
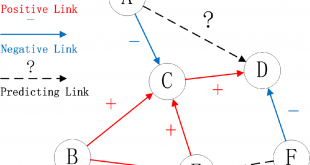
4- الگوریتم های پیشبینی ارتباطات در تحلیل شبکه های اجتماعی
پیشبینی لینک یا وجود ارتباط میان دو موجودیت بر اساس ویژگیهای موجودیتها و دیگر لینکهای مشاهده شده در گراف را پیشبینی لینک[۱] میگویند . یا به عبارت دیگر اگر در زمان n0 یک تصویر لحظهای از مجموعه لینکها داشته باشیم، هدف پیشبینی لینکها در زمان n1 میباشد.

الگوریتم های پیشبینی ارتباطات یا Link Prediction سه قابلیت مهم را در اختیار ما قرار میدهد:
۱- پیشبینی ارتباطاتی که ممکن است در آینده ایجاد شوند
۲- کشف ارتباطات گم شده که به هر دلیل در زمان جمع آوری اطلاعات از دست رفته اند
۳- کشف ارتباطات پنهان یعنی رابطه هایی که وجود دارد ولی اثر از آن در داده ها نیست
-
روشهای مختلف پیشبینی لینک
میتوان روشهای مختلف پیشبینی لینک را به دو دسته کلی تقسیمبندی نمود. دسته اول روشهایی هستند که بدون بررسی پیش زمینه روند به وجود آمدن لینکها در گذشته، تنها به کمک ویژگیهای ساختاری موجود در گراف شبکه به پیشبینی لینکها در آینده میپردازند. ابن دسته را میتوان روشهای بدون ناظر در نظر گرفت. دسته دوم از روشها پس از یادگیری[۱] یک یا چند مرحله از فرآیند به وجود آمدن لینکها در گذشته، به پیشبینی لینک میپردازند. این دسته از روشها را میتوان روشهای پیشبینی لینک باناظر نامگذاری نمود.
الگوریتمهای پیشبینی لینک بدون ناظر غالباً از ویژگیهای ساختاری منجمله تعداد همسایههای مشترک، طول کوتاهترین مسیر میان دو گره، درجه دو گره و از این قبیل ویژگیهای ساختاری موجود در گراف شبکههای اجتماعی استفاده مینمایند. که میتوان دسته بندی زیر را برای آن در نظر گرفت.
مبتنی بر همسایه مشترک
- آدامیک آدارAdamic and Adar
- اختصاص منابع Resource Allocation
- شباهت کسینوسی Cosine Similarity
- SimRank
- CommonNeighbor
- ضریب جاکارد Jaccard’s Coefficient
- اندیس سورنسن Sørensen Index
مبتنی بر مسیر یا فاصله Distance (فاصله کمتر احتمال ارتباط بیشتر)
- روشهای مبتنی بر گام تصادفی
- Rooted PageRank
- Katz
مبتنی بر درجه (درجه های بیشتر احتمال ارتباط بیشتر)
- Preferential Attachment
الگوریتمهای پیشبینی لینک باناظر گاهی اوقات با یادگیری پارامترهای یک مدل احتمالاتی و یا بررسی روند تکامل یک زیرساختار خاص در گراف شبکه به پیشبینی لینک میپردازند. در مجموع هر روشی که به نوعی شباهت دو گره را نسبت به یکدیگر در گراف شبکه نشان دهد را میتوان به نوعی برای پیشبینی لینک نیز استفاده نمود. الگوریتم های مطرح در حوزه پیشبینی لینک در شبکه های اجتماعی عبارتند از:
- Adamic Adar
- Common Neighbors
- Cosine Similarity
- Jaccard Coefficient
- Resource Allocation
- Sourensen Index
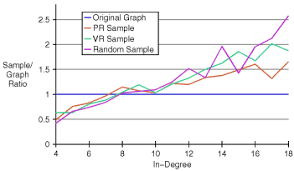
۵- الگوریتم های نمومه برداری گراف در تحلیل شبکه های اجتماعی
شبکه های اجتماعی معمولا شامل تعداد زیادی نود هستند. در نتیجه گراف ناشی از این شبکهها بسیار بزرگ بوده و طبیعتا گرافهای بزرگ این چنینی هزینه پردازش زیادی دارند. در این گونه گرافها حتی الگوریتمهای از مرتبه O(n2) هم دارای پیچیدگی بالایی محسوب میشوند. زیرا بعنوان مثال گرافی حاوی یک میلیون نود با الگوریتم از مرتبه n2 هم نیاز به هزار میلیارد محاسبه دارد!
طبیعتا بهترین راه حل برای این گونه مسایل در ابتدا یافتن الگوریتمهای بهتر از مرتبه پایین تر است. در این صورت راه حل یافت شده امکان پردازش گرافهای بزرگ را در زمانی معقول میدهند و باعث فراتر رفتن دامنه پردازشهای ممکن به گرافهای عظیمتر میشوند. برای مطالعه بیشتر در این زمینه به مبحث نمومه برداری گراف در شبکه های اجتماعی مراجعه کنید. اما به هر حال ممکن است یافتن چنین الگوریتمهایی دشوار اگر نه غیر ممکن باشد. یکی از راههای حل مسایل پیچیده محاسباتی برای پردازش گرافهای بزرگ، محاسبه تقریبی پارامترها است. این محاسبات تقریبی میتواند به دو صورت انجام پذیرد:
- محاسبه تقریبی روی گراف اصلی
- محاسبه دقیق روی گراف فرعی شبیه به گراف اصلی (همان نمونه برداری گراف)
نکات مهم در نمونه برداری گراف
نکته مهم در نمونه برداری انتخاب جمعیت نمونه است. در نمونه برداری سعی میشود نمونه جمعیت انتخاب شده تا حد امکان نااریب باشد تا پارامترهای محاسبه شده به واقعیت نزدیکتر باشند. در صورتی که نمونه برداری کاملا تصادفی نباشد امکان دارد نمونه جمع آوری شده ویژگیهای زیر مجموعه ای از کل جمعیت را انعکاس دهد و قابل تعمیم به کل جمعیت نباشد. در این صورت تخمین های صورت گرفته اریب و متمایل به سمت یک زیر مجموعه ای باشد که گویای کل جمعیت نباشد.
در نتیجه مساله اصلی در نمونه برداری از گراف، الگوریتم و روش انتخاب نمونهها و روش پیمایش گراف برای یافتن نمونههای بعدی است. سوالاتی که در این میان باید پاسخ داده شوند بدین قرار میباشند:
- چه راهکار نمونه برداری را مورد استفاده قرار دهیم؟
- اندازه گراف نمونه تا چه حد میتواند کوچک شود؟
- چگونه مقادیر بدست آمده برای گراف نمونه را به گراف بزرگ تعمیم دهیم؟
در هر صورت هدف اصلی ما در نمونه برداری گراف این است که ویژگیهای گراف نمونه تا حد امکان به گراف اصلی نزدیک باشد و یا بهتر است بگوییم ویژگیهای گراف اصلی به نحو دقیقتری قابل محاسبه از گراف فرعی باشد.
تکنیکهای ارزیابی در نمونه برداری گراف
مساله بعد، لیستی از خصوصیات گراف اولیه است که میخواهیم در گراف نمونه آن ویژگیها را حفظ کنیم. هدف ما در اینجا این نیست که یک روش مدل سازی بیابیم که تنها یکی از خصوصیات گراف را حفظ کند ما به دنبال این هستیم که یک روش جامع و مانع برای مدل سازی پیدا کنیم که با تمامی خصوصیات گراف مطابقت کند تا در نتیجه گرافهای نمونه را بتوان به عنوان نمونه ای از مدل های پیچیده و هزینهبر استفاده کرد.
معیارهای ارزیابی یک گراف ایستا
گراف ایستا گرافی است که در طول زمان تغییر نمیکند یا تغییرات آن ناچیز شمرده میشود. گرافها معمولا تغییر دارند و در طول زمان تغییر میکنند. اما در یک بازه زمانی کوتاه مدت میتوان آنها را ایستا فرض کرد. پس اگر یک تصویر (snapshot) مربوطه به زمان خاصی از تکامل گراف موجود باشد میتوان به دیده گراف ایستا به آن نگاه کرد. حال با فرض داشتن یک تصویر ایستا از گراف میتوانیم ویژگی های زیر را روی آن محاسبه کرده و برای مقایسه گراف و نمونه برداشته شده از آن استفاده کنیم:
- توزیع درجه ورودی نودها (In-Degree Ditribution): برای این معیار هیستوگرام درجه ورودی نودها، یعنی درصد نودهایی که درجه ورودی خاصی دارند را شمارش میکنیم. توزیع درجه شبکه های اجتماعی معمولا از توزیع توانی (power law) تبعیت میکند.
- توزیع درجه خروجی (Out-degree): مشابه توزیع درجه ورودی با این تفاوت که بجای درجه ورودی شمارش بر روی درجه خروجی نودها انجام میگیرد.
- توزیع تعداد اجزای دارای همبندی ضعیف گراف (Weakly connected components) : دو نود در صورتی با ارتباط ضعیف به هم وصل شده اند که بین این دو نود حداقل یک مسیر چه از نود اول به دوم چه بالعکس وجود داشته باشد.
- توزیع تعداد اجزای قویا همبند گراف (Strongly connected components): اجزای قویا مرتبط زیر مجموعه ای از اجزای دارای همبندی ضعیف هستند که بین هر دو نود هم مسیری از نود اول به دوم و هم مسیری از نود دوم به اول وجود داشته باشد. توجه داشته باشیم که اجزای دارای همبندی قوی حتما دارای همبندی ضعیف هستند اما عکس آن برقرار نیست.
- Hop-Plot: توزیع تعداد نودهایی که در h گام به همدیگر دسترسی دارند.
- Hop-Plot روی بزرگترین جزء دارای همبندی ضعیف
- توزیع اولین بردار تکینه سمت چپ ماتریس مجاورت نسبت به رتبه
- توزیع مقادیر ویژه ماتریس مجاورت نسبت به رتبه که معمولا دارای توزیع دم پهن (heavy-tail) است.
- توزیع ضریب خوشه بندی[۹] گراف. ضریب خوشه بندی، یک کسر است و عبارت است از تعداد لینکهای موجود میان دوستان یک نود تقسیم بر تعداد لینکهای ممکن.
معیارهای ارزیابی تکامل زمانی گراف
وقتی که تصاویر مختلفی از تکامل یک گراف در طول زمان داشته باشیم علاوه بر این که معیارهای فوق را میتوانیم روی هر تصویر محاسبه و با هم مقایسه کنیم الگوی تغییر برخی ویژگی ها در طول زمان نیز امکان پذیر میشود. برای انجام این مقایسه، ما اصولا یک عدد اسکالر (مانند قطر گراف) را برای هر تصویر محاسبه کرده و بررسی کنیم این عدد با افزایش اندازه گراف چه تغییراتی کرده است.
معیارهای مقایسه تکامل زمانی گرافها به قرار زیر میباشد:
- Densification Power law: نسبت تعداد یالها روی تعداد نودها در طول زمان. این قانون ادعا میکند که e(t) یعنی تعداد یالها در زمان t دارای توزیعی متناسب با n(t)a است که n(t) تعداد نودها در زمان t است. توان a معمولا بزرگتر از یک است و این یعنی این که متوسط درجه نودها در طول زمان افزایش پیدا میکند.
- قطر موثر گراف در طول زمان، که عبارت است از حداقل تعداد گامی است که ۹۰ درصد از نودهای گراف بتوانند در گامهایی کمتر یا مساوی آن تعداد گام به یکدیگر دسترسی داشته باشند. مشاهده شده که قطر موثر در طول زمان کاهش می یابد و یا ثابت میماند.
- تغییرات اندازه نرمالیزه شده بزرگترین جزء همبند گراف در طول زمان: که عبارت است از تعداد نودهای موجود در بزرگترین جزء همبند تقسیم بر تعداد کل نودها.
- بزرگترین مقدار تکینه (singular value) ماتریس مجاورت گراف در طول زمان
- میانگین ضریب خوشهبندی نودها در طول زمان.
برای مطالعه بیشتر در این زمینه به مبحث پیشبینی لینک در شبکه های اجتماعی مراجعه کنید.
۶- تحلیل انتشار در تحلیل شبکه های اجتماعی
افرادی که در یک شبکه اجتماعی عضو هستند، موارد متعددی را مورد بحث قرار میدهند و اطلاعات مختلفی را داوطلبانه یا ناخواسته یا باهدف انتشار آن به مخاطبان وسیعی یا در یک حلقه دوستانه منتشر میکنند و میتوان گفت که شبکههای اجتماعی نقش مهمی در انتشار اطلاعات و به اشتراکگذاری اطلاعات دارد. با توجه به این خصوصیت شبکه اجتماعی، طبیعی است که از آن برای به حداکثر رساندن فروش محصولات خود بهرهبرداری کنند
یک روش که توسط شرکتها مورد استفاده میگیرد، مبتنی بر بازاریابی ویروسی است که مشتریان موجود در بازار محصولات را در میان دوستان خود قرار میدهند. مبارزات انتخاباتی مثال دیگری است که در آن یک نگاه خاص یا یک مجموعهای از نگاهها به برخی مخاطبان ارائه میشود و ازاینرو، این دیدگاهها از طریق مخاطبان پخش میشود. این معمولاً توسط تبادل پیام بین کاربران و یا زنجیرهای از نفوذ از طریق دهانبهدهان (Word Of Mouth) به دست میآید.
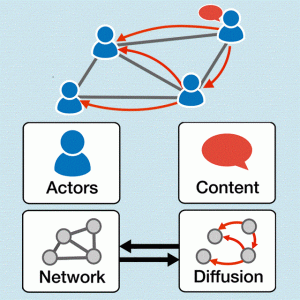
پروژه تحلیل انتشار اطلاعات بهطورکلی وظیفه تشخیص جریانهای مخفی اطلاعات در درون محتوی متنی که درواقع شاهراههای اطلاعاتی هستند را بهصورت یک گراف وزندار بر عهده دارد. وزن یالهای این گراف درواقع نشانگر میزان سرعت(عکس لختی زمان ) انتقال اطلاعات از طریق یال مربوطه است. و گرههای این گراف نشاندهنده تارنماهای تأثیرگذار در انتشار اطلاعات درون شبکه است که هر یک از این تارنماها با توجه به رفتار خود در برخورد با جریان اطلاعاتی میتواند نقشی متفاوت داشته باشد. این نقشها شامل تولیدکننده اطلاعات، مصرفکننده اطلاعات و انتقالدهنده اطلاعات هستند. این وظیفه با استخراج خصوصیات منفرد هر جریان اطلاعاتی(که در این سند به آنها آبشارهای اطلاعاتی هم گفته میشود) و گره های دخیل در آن جریان تکمیل میگردد.
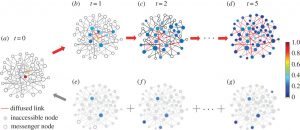
مدل های انتشار
مدل انتشار، همچنین بهعنوان روشهای انتشار نیز شناخته میشود، کل فرآیند انتشار را شرح و تعیین میکند که چگونه نفوذ از طریق شبکه پخش میشود. نقش این مدل انتشار در درجه اول، تکرار یا شبیهسازی روند انتشار واقعی زندگی است و تعیین میکند که کدام گرهها توسط مجموعهای از گرههای آغازگر فعال میشوند. دو روش کلی برای مدلهای انتشار که مبتنی بر توپولوژیک شبکه هستند وجود دارد که در زیر مشهورترین آنها توضیح داده شده است .
- روش های مبتنی بر توپولوژی
- روش اکتشافی
- روش حریصانه
- مدل انتشار مستقل IC
- مدل آستانه خطی LT
- روش انتشار گرما HD
- مدل اپیدمیولوژی
- مدل انتشار فعالیت
روش های مبتنی بر توپولوژی
توپولوژی در لغت به معنای نگاشت یک فضا به هندسه مکانی است. توپولوژی آرایشی از عناصر مختلف مانند یالها و گرهها در یک ارتباط است. توپولوژی را توپولوژیک ساختار یک شبکه نیز میدانند. اکثر روشهای شناسایی گرههای مؤثر مبتنی بر اتصالات توپولوژیکی گرههای شبکههای اجتماعی هستند. بر اساس ساختار، شبکه مشخصههای مختلفی پیدا میکند ازجمله قطر، مثلثها، توزیع درجه، آنتروپی و غیره. این خصوصیات، توپولوژیک یک شبکه را تعریف میکند. یعنی شبکه از این توپولوژی برخوردار است. بدین منظور که چگونگی انتقال و انتشار اطلاعات از گرهها به یکدیگر را توپولوژیک یک شبکه تعیین میکند که دلیل آن تعیین کردن نقشهای گرهها در شبکه توسط توپولوژی آن است.
برای مطالعه بیشتر در این زمینه به مبحث تحلیل انتشار در شبکه های اجتماعی مراجعه کنید.
آدرس کانال تلگرام سایت بیگ دیتا:
آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel
جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.
جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.
Views: 13958
برچسبcentrality SNA Social Network Analysis آنالیز شبکه های اجتماعی بصری سازی پیشبینی ارتباطات پیشبینی لینک تحلیل انتشار تحلیل شبکه های اجتماعی تحلیل گراف تشخیص انجمن ها خوشه بندی گراف خوشهبندی سلسله مراتبی رسانه های اجتماعی شبکه های اجتماعی گراف کاوی مرکزیت نمومه برداری گراف
همچنین ببینید
بیش ازصد موجودت اسمی برای تشخیص رویداد (Event Detection)
تشخیص رویداد: رصد شبکه های اجتماعی، رویدادهای دنیای واقعی را نشان میدهد و اطلاعات ارزشمندی …
مجموعه داده (dataset) گراف شبکه جاده ای پنسیلوانیا
اطلاعات مجموعه داده (dataset) گراف شبکه جاده پنسیلوانیا یکی از کاربرد های تحلیل شبکه های …
یک دیدگاه
دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.
 خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم
خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم












سلام
درخصوص نحوه واکشی اطلاعات و دیتا از شبکه های اجتماعی مطالبی دارید؟ مثلا کد یا روش خاصی که بتوان به دینارهای مختلف درشبکه های اجتماعی مختلف نظیر اینستاگرام یا توییتر و غیره دست یافت؟