آموزش کامل شبکه عصبی ( artificial neural network) و نحوه استفاده آن
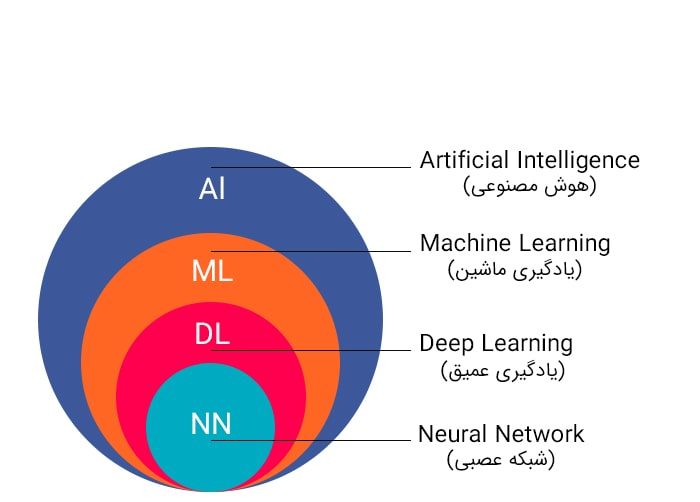
از چند دهه گذشته که رایانهها امکان پیادهسازی الگوریتمهای محاسباتی را فراهم ساختهاند، در راستای شبیهسازی رفتار محاسباتی مغز انسان، کارهای پژوهشی بسیاری از سوی متخصصین علوم رایانه، مهندسین و همچنین ریاضیدانها شروع شده است، که نتایج کار آنها، در شاخهای از علم هوش مصنوعی و در زیرشاخه هوش محاسباتی تحت عنوان موضوع «شبکه های عصبی مصنوعی» یا Artificial Neural Networks (به اختصار: ANNs) طبقه بندی شده است. در مبحث شبکه های عصبی مصنوعی، مدل های ریاضی و نرمافزاری متعددی با الهام گرفتن از مغز انسان پیشنهاد شدهاند، که برای حل گستره وسیعی از مسائل علمی، مهندسی و کاربردی، در حوزه های مختلف کاربرد دارند.
عناوين مطالب: '
کاربردهای شبکه های عصبی
ANN ها به دلیل توانایی در بازتولید و مدل سازی فرایندهای غیر خطی در رشته های مختلفی کاربرد یافته اند. برخی زمینه های کاربردی عبارت اند از شناسایی سیستم و کنترل (کنترل وسیله نقلیه، پیش بینی مسیر، کنترل فرایند، مدیریت منابع طبیعی)، شیمی کوانتومی، بازی و تصمیم گیری (تخته نرد، شطرنج، پوکر)، الگوشناسی (سیستم های رادار، شناسایی چهره، دسته بندی سیگنال، شناسایی اشیاء و غیره)، شناسایی دنباله ای (ژست، صحبت، شناسایی نوشته با دست)، تشخیص پزشکی، امور مالی (مثلاً سیستم های تجاری خودکار)، داده کاوی، بصری سازی، ترجمه ماشین، فیلترینگ شبکه های اجتماعی و فیلترینگ ایمل های اسپم.
ANN ها در شناسایی سرطان، از جمله سرطان های ریه، پروستات، روده بزرگ و نیز تشخیص خطوط سلول های سرطانی تهاجمی از خطوطی که کمتر تهاجمی هستند تنها با استفاده از اطلاعات شکل سلول، مورد کاربرد قرار گرفته اند. ANN ها همچنین برای ساختن مدل های جعبه سیاه در علوم زمین شناسی استفاده شده اند: هیدرولوژی، مدل سازی اقیانوس و مهندسی سواحل، و ژئوموفولوژی تنها چند مثال از این نوع هستند.
تاریخچه شبکه های عصبی مصنوعی
وارن مک کولاچ و والتر پیتس(Warren McCulloch and Walter Pitts) (1943) مدلی محاسباتی برای شبکه های عصبی، مبتنی بر ریاضیات و الگوریتم هایی به نام منطق آستانه، ابداع کردند. این مدل، مسیر را برای تقسیم پژوهش های شبکه های عصبی به دو روش، هموار کرد. یک روش، بر فرایندهای زیستی در مغز تمرکز کرد و دیگری بر کاربرد شبکه های عصبی در هوش مصنوعی تمرکز داشت. این عمل، به شبکه های عصب محیطی (nerve networks) و ارتباط آن ها به ماشین های متناهی منجر شد.
عملکرد عصب بیولوژیکی
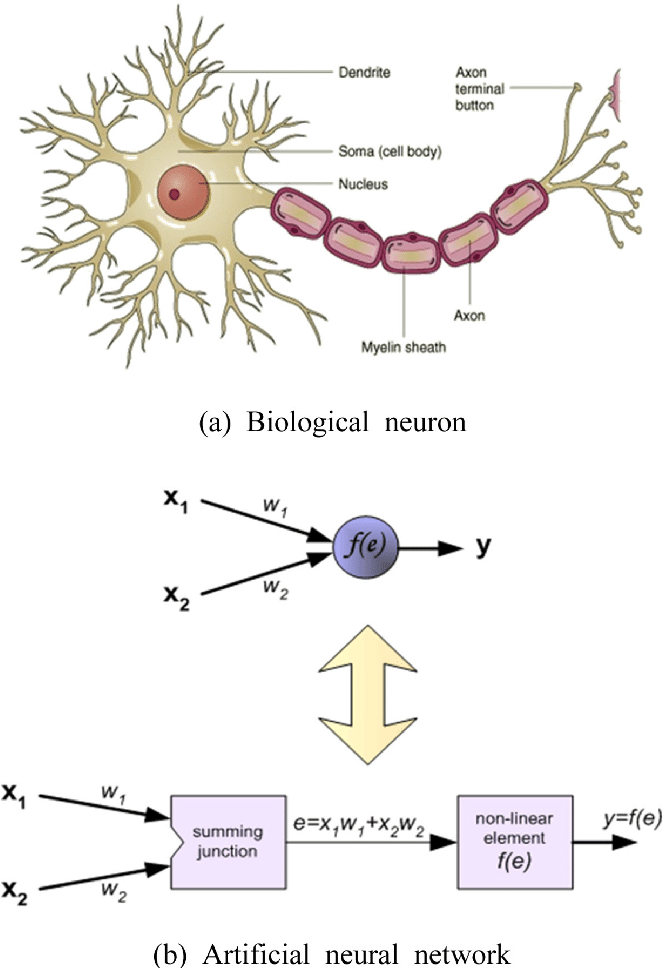
مغزِ انسان در خود تعداد بسیار زیادی از نورونها را جای داده است تا اطلاعاتِ مختلف را پردازش کرده و جهانِ اطراف را بشناسد. به صورت ساده، نورونها در مغزِ انسان اطلاعات را از نورونهای دیگر به وسیلهی دندرویدها میگیرند. این نورونها اطلاعاتِ ورودی را با هم جمع کرده و اگر از یک حدِ آستانهای فراتر رود به اصلاح فعال (Fire) میشود و این سیگنالِ فعالْ شده از طریق آکسونها به نرونهای دیگر متصل میشود.
مدل شبکه عصبی
در تصویر زیر پنج عنصر وجود دارد:
اول Xها هستند. اینها همان ورودیهای ما (نرون های ورودی) هستند که از مجموعهی دادهها استفاده میکنند. در واقع ورودیِ الگوریتم همینها Xها هستند که در این تصویر از X1 تا Xn وجود دارند.
عناصرِ دومْ وزنها هستند. در شبکههای عصبی هر کدام از Xها یک وزن دارد که با W نمایش میدهیم. همانطور که مشاهده میکنید هر کدام از ورودیهای ما به یک وزن متصل شده است. در واقع هر ورودی بایستی در وزنِ خود ضرب شود. (مثل X1 که یک وزن به اسم W1 دارد)
عنصرِ سوم در شبکهی عصبی تابع جمع (سیگما) است. که حاصلِ ضربِ Xها در Wها را با هم جمع میکند.
عنصر چهارم یک تابع فعالسازی است که فعلاً در این درس به دلیل سادهسازیِ مطلب به آن نمیپردازیم (در درسهای آینده حتماً به تابعِ فعالسازی خواهیم پرداخت)
عنصرِ پنجم و آخر نیز خروجیِ شبکهی عصبی است که در واقع نتیجهی این شبکه را مشخص میکند.
فرض کنید به یک بچهی کوچک میخواهید آموزش بدهید. مثلاً میخواهید به او بگویید که فرق گربه با سگ چیست؟ برای این کار چه کاری میکنید؟ یک راهِ ساده (که خودِ ما هم خیلی چیزها را از همین طریق یاد گرفتهایم) این است که به بچهی کوچک بگوییم مثلاً این گربه است و آن گربه نیست. چندین مورد گربه را به بچه نشان میدهیم و چندین موردی که گربه نیست را هم به او میگوییم. به راحتی یک بچه با چند بار تمرین میتواند یاد بگیرد که گربه چیست! یعنی میتواند تمایزِ گربه را با بقیه حیوانات دیگر درک کند. این روش پایهی روشِ یادگیری در پرسپترون و بسیاری دیگر از الگوریتمهای دادهکاوی است.
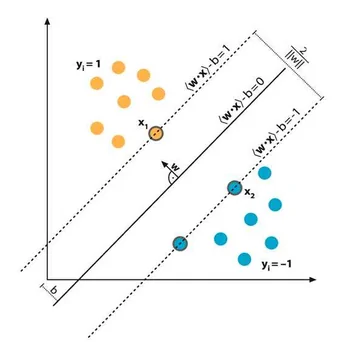
فرمول زیر را برای دو ورودیِ X1 و X2 که ضرب ورودی در وزنها بود، به خاطر بیاورید:
W1*X1 + W2*X2 + θ = ۰
فرمولِ بالا زیاد سخت نیست. ابتدا X1 را در وزن W1 ضرب کردهایم (برای X2 و W2 هم همینطور) سپس آنها را با هم جمع کردهایم. این معادله مارا یاد معادلهی خط می اندازد. حال فرض کنید که W1 و W2 دو عددِ ثابت هستند که همانطور که میدانید شیبِ خط نام دارند. θ هم که اگر یادتان باشد عرض از مبدا است. این خط به یادگیریِ پرسپترون کمک میکند و موجب تفکیک ویژگیها می شود.
قاعده یادگیری
قاعده یادگیری، قانون یا الگوریتمی است که به منظور اینکه یک ورودی داده شده به شکبه، خروجی مطلوب را تولید کند، پارامترهای شبکه عصبی را اصلاح می نماید. این فرایند یادگیری معمولاً در اصلاح کردن وزن ها و آستانه های متغیرهای درون شبکه خلاصه می شود.
شبکه عصبی به عنوان تابع
مدل های شبکه عصبی را می توان به عنوان مدل های ساده ریاضی در نظر گرفت که یک تابع f:X→Y یا توزیعی روی X یا هر دوی X و Y تعریف می کند. گاهی اوقات مدل ها ارتباط تنگاتنگی با یک قاعده یادگیری دارند. یکی از کاربردهای رایج عبارت “مدل ANN” در حقیقت تعریف کلاس چنین توابعی است (که در آن اعضای کلاس با تغییر در پارامتر، وزن های اتصال یا ویژگی های معماری از قبیل تعداد نورون ها یا اتصالات آن ها بدست می آیند.)
از نظر ریاضی، تابع f(x) شبکه یک نورون به عنوان ترکیبی از توابع gi(x) دیگر تعریف می شود که خود قابل تجزیه به توابع دیگری هستند. این عمل به شکل مطلوبی توسط یک ساختار شبکه ای قابل نمایش است، که در آن پیکان ها نشانگر وابستگی میان توابع است.
یک نوع ترکیب پرکاربرد، جمع وزندار غیر خطی f(x)=K(∑iwigi(x)) است که در آن K (که عموماً از آن به نام تابع فعال سازی یاد می شود) یک تابع پیشگو مثل تانژانت هذلولوی یا تابع سیگموئید یا تابع بیشینه هموار یا تابع یکسوسازاست. ویژگی مهم تابع فعال ساز این است که جابه جایی همواری را در اثر تغییر مقادیر ورودی ایجاد می کند، به عبارت دیگر، تغییری اندک در ورودی، باعث ایجاد تغییری اندک در خروجی می شود. در ادامه، به گردایه ای از توابع gi به عنوان یک بردار:
g=(g1,g2,…,gn)
نگاه میکنیم.
یادگیری شبکه
امکان یادگیری، بیشترین توجه را در شبکه های عصبی به خود جلب کرده است. با داشتن یک کار (یا فعالیت) (task) برای انجام، و کلاسی از توابع به نام F، یادگیری به معنای استفاده از مجموعه ای از مشاهدات برای پیدا کردن f*∈F است که کار را نسبت به یک معیار بهینگی، انجام دهد.
این مطلب مستلزم تعریف یک تابع هزینه C:F→R است بطوریکه به ازای جواب بهینه *f داشته باشیم:
C(f*)≤C(f) ∀f∈F
یعنی، هیچ جوابی هزینه ای کمتر از هزینه جواب بهینه ندارد (بهینه سازی ریاضی را ببینید).
تابع هزینه C مفومی مهم در یادگیری است، زیرا معیاری است که نشان می دهد یک جواب خاص، چه اندازه از جواب بیهنه مسئله ای که باید حل شود دور است. الگوریتم های یادگیری در فضای جواب ها دنبال تابعی می گردند که کمترین هزینه ممکن را داشته باشد.
در کاربردهایی که جواب به داده ها وابستگی دارد، هزینه لزوماً باید تابعی از مشاهدات باشد، در غیر این صورت مدل به داده ها ربطی نخواهد داشت. معمولاً هزینه به عنوان یک آماره که تنها می توان آن را تقریب زد، تعریف می شود.
به عنوان مثالی ساده، مسئله پیدا کردن مدل f را در نظر بگیرید که C=E [ (f(x)-y)2 ] را برای زوج های مرتب داده (x,y) از یک توزیع D کمینه سازی می کند. در عمل تنها N نمونه از D را در اختیار داریم و لذا، برای مثال فوق، تنها عبارت زیر را کمینه سازی می کنیم:
C^=۱N∑iN(f(xi)–yi)۲
بنابراین، هزینه روی نمونه ای از داده ها کمینه سازی می شود نه روی کل توزیع.
وقتی که ∞ → N شکلی از یادگیری ماشین برخط (online) باید استفاده شود، که در آن هزینه با مشاهده هر مثال جدید کاهش می یابد. در حالی که یادگیری ماشین برخط اغلب هنگامی استفاده می شود که D ثابت است، اما بیشترین اثربخشی را هنگامی دارد که توزیع با زمان به کُندی تغییر کند. در روش های شبکه های عصبی، اغلب نوعی از یادگیری ماشین برخط برای پایگاه های داده متناهی استفاده می شود.
انتخاب تابع هزینه شبکه
اگرچه می توان یک تابع هزینه اد هاک (تک کاره) تعریف نمود، اما اغلب یک (تابع) هزینه مخصوص مورد استفاده قرار می گیرد، چه به این خاطر که دارای خواص مطلوبی (مثل تحدب) است، چه به این دلیل که بطور طبیعی از فرمول بندی خاصی از مسئله بوجود می آید (مثلاً، در یک فرمول بندی احتمالاتی، احتمال پسینِ مدل را می توان به عنوان هزینه معکوس استفاده کرد). در نهایت، تابع هزینه به کار (task) مورد نظر بستگی دارد.
مشکلات آموزش شبکه
انتقادی که معمولاً به شبکه های عصبی وارد است، به ویژه در رباتیک، این است که برای عمل در دنیای واقعی به آموزش زیادی نیاز دارند. برخی راه حل های بالقوه عبارت اند از بُر زدن تصادفی مثال های آموزشی توسط یک الگوریتم بهینه سازی عددی که هنگام تغییر دادن اتصالات شبکه به دنبال یک مثال، گام های زیادی را بر ندارد، و نیز روش معروف گروه بندی مثال ها در دسته های کوچک. بهبود کارایی آموزش و توانایی همگرایی همواره زمینه پژوهشی فعالی برای شبکه های عصبی بوده است. برای مثال، با معرفی یگ الگوریتم بازگشتی کمترین مربعات برای شبکه عصبی CMAC، فرایند آموزش تنها با یک گام به همگرایی می رسد. همچنین هیچ شبکه عصبی ای مسائل محاسباتی دشوار مثل مسأله چند وزیر، فروشنده دوره گرد یا تجزیه اعداد صحیح بزرگ را حل نکرده است.
شبکه های عصبی بزرگ و اثربخش به منابع محاسباتی قابل ملاحظه ای نیاز دارند. در حالیکه مغز توسط گرافی از نورون ها، سخت افزاری را بر فعالیت پردازش سیگنال منطبق کرده است، حتی شبیه سازی یک نورون ساده شده روی معماری ون نویمن (von Neumann) ممکن است یک طراح شبکه عصبی را وادار به پُر کردن میلیون ها سطر پایگاه داده برای اتصالات آن کند – چیزی که می تواند میزان زیادی حافظه و ذخیره سازی به خود اختصاص دهد. علاوه بر آن، طراح اغلب باید سیگنال ها را در بسیاری از این اتصالات و نورون های مربوطه منتقل کند – چیزی که معمولاً قدرت و زمان محاسباتی زیادی از CPU طلب می کند.
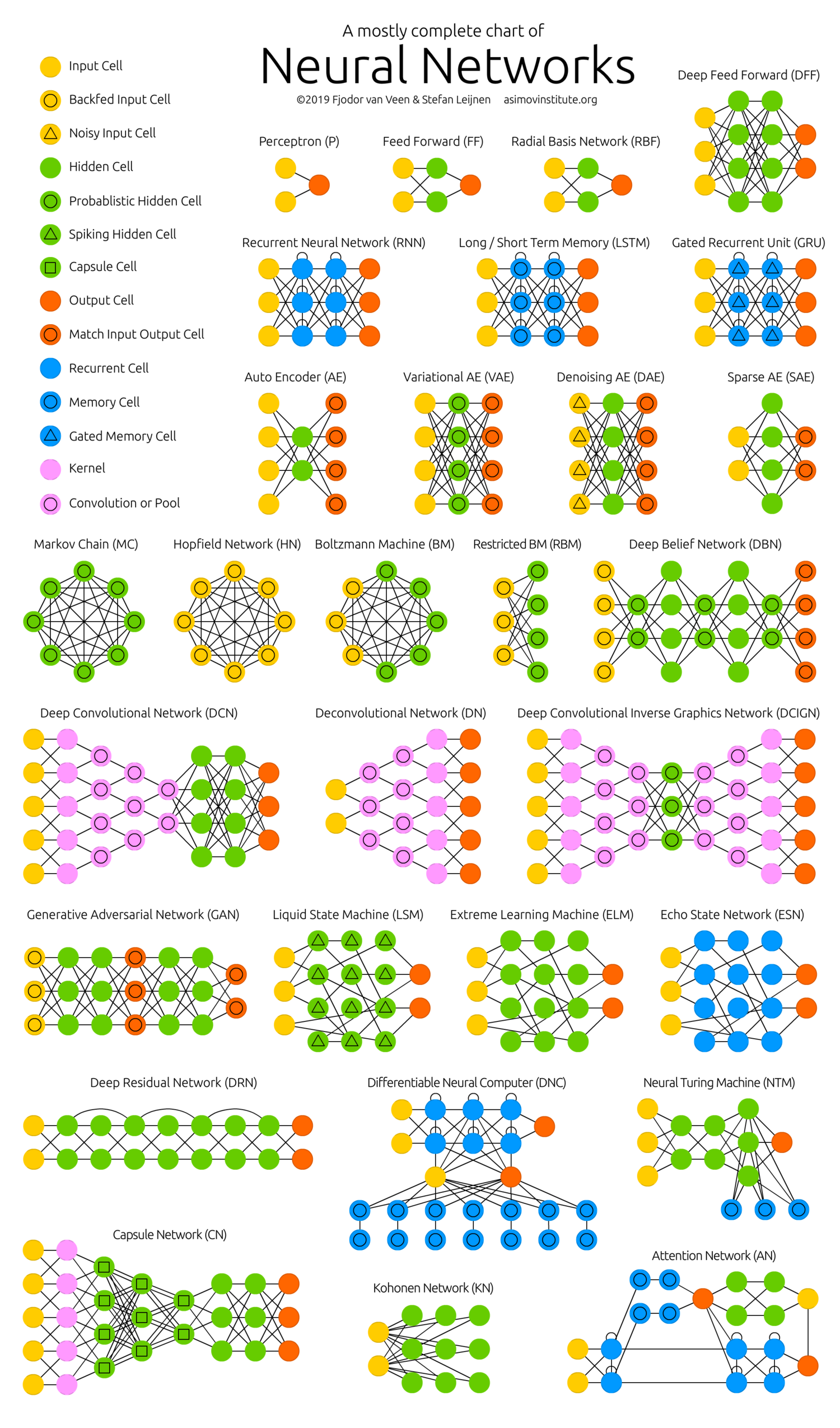
انواع شبکه های عصبی
آدرس کانال تلگرام سایت بیگ دیتا:
آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel
جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.
جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.
Views: 1577
برچسبANN artificial neural network SPSS شبکه عصبی شبکه های عصبی
همچنین ببینید
روش های داده کاوی (Data Mining) به زبان ساده
امروزه داده کاوی به عنوان پایه و مبنای تصمیم های مهم محسوب میشود. داده کاوی …
 خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم
خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم