نمونه برداری گراف شبکه های اجتماعی

شبکه های اجتماعی معمولا شامل تعداد زیادی نود هستند. در نتیجه گراف ناشی از این شبکه‌ها بسیار بزرگ بوده و طبیعتا گرافهای بزرگ این چنینی هزینه پردازش زیادی دارند. در این گونه گرافها حتی الگوریتمهای از مرتبه O(n²)  هم دارای پیچیدگی بالایی محسوب میشوند. زیرا بعنوان مثال گرافی حاوی یک میلیون نود با الگوریتم از مرتبه n² هم نیاز به هزار میلیارد محاسبه دارد! طبیعتا بهترین راه حل برای این گونه مسایل در ابتدا یافتن الگوریتمهای بهتر از مرتبه پایین تر است. در این صورت راه حل یافت شده امکان پردازش گرافهای بزرگ را در زمانی معقول میدهند و باعث فراتر رفتن دامنه پردازشهای ممکن به گرافهای عظیم‌تر می‌شوند. اما بهر حال ممکن است یافتن چنین الگوریتمهایی دشوار اگر نه غیر ممکن باشد.

نمونه برداری گراف:

علاوه بر استفاده از تکنولوژی های مربوط به دخیره سازی و گراف های حجیم مثل تایتان  و تکنولوژی های مربوط به پردازش گراف های حجیم مثل گرافچی یکی دیگر از راه‌های حل مسایل پیچیده محاسباتی برای پردازش گرافهای بزرگ، محاسبه تقریبی پارامترها است. این محاسبات تقریبی میتواند به دو صورت انجام پذیرد:

• محاسبه تقریبی روی گراف اصلی
• محاسبه دقیق روی گراف فرعی شبیه به گراف اصلی (همان نمونه برداری گراف)

محاسبه تقریبی روی گراف اصلی با استفاده از الگوریتمهای تقریبی (approximation) که ساده شده الگوریتمهای دقیق هستند صورت میپذیرد. مطالعه این روشها شاخه وسیعی در علوم کامپیوتری هستند و منظور نظر این گزارش نیستند.

محاسبه تقریبی از نوع دوم بر روی گراف فرعی شبیه به گراف اصلی صورت میپذیرد که به عنوان نمونه برداری گراف از آن یاد میشود. در این روشها الگوریتم مورد استفاده همان الگوریتمی است که احیانا از  مرتبه پیچیدگی بالایی نیز برخوردار است اما در صورت کوچک بودن اندازه گراف، قابل محاسبه بر روی کامپیوترهای معمولی در مدت زمانی معقول است.

گراف فرعی با ساده کردن گراف اصلی بدست می‌آید. برای ساده کردن گراف راه‌های متعددی وجود دارد. در برخی کاربردها ممکن است حذف نودهای غیرمهم که احیانا درصد زیادی از نودها را تشکیل خواهند داد یک کار معقول باشد.

در برخی کاربردها ممکن است گروه بندی چند نود و جایگزین کردن آنها با یک سوپرنود مناسب تحلیل باشد و باعث کوچک شدن گراف همراه با حفظ اطلاعات مهم و لازم شود. در این کار، الگوریتمهای تشخیص انجمنها و کاهش گراف به گراف ارتباط انجمنها نقش مهمی را ایفا میکند.

روش دیگر استفاده از روشهای کاهش بعد در گراف است. در این روشها معمولا ماتریس مجاورت گراف با روشهای جبر خطی ساده شده و محورهای اصلی ماتریس با استفاده از بردارها و مقادیر ویژه مشخص میشود و با استفاده از انتخاب درصدی از بزرگترین مقادیر ویژه ابعاد گراف کوچکتر میشود.

روش دیگر ساده کردن گراف، استفاده از تجربه آماردانان در این مورد است. نهادهای آمار و سرشماری برای کاهش هزینه سرشماری سعی میکنند پارمترهای یک جمعیت بزرگ همانند جمعیت کشور را از روی نمونه‌های نسبتا کوچک آماری تخمین بزنند. همین کار اگر به درستی بر روی یک گراف صورت گیرد میتواند نمونه کوچک فرعی از گراف بزرگ اصلی استخراج کند و محاسبات بر روی این گراف کوچک که قاعدتا ساده تر است صورت گیرد.

نکات مهم در نمونه برداری گراف

نکته مهم در نمونه برداری انتخاب جمعیت نمونه است. در نمونه برداری سعی میشود نمونه جمعیت انتخاب شده تا حد امکان نااریب باشد تا پارامترهای محاسبه شده به واقعیت نزدیک‌تر باشند. در صورتی که نمونه برداری کاملا تصادفی نباشد امکان دارد نمونه جمع آوری شده ویژگی‌های زیر مجموعه ای از کل جمعیت را انعکاس دهد و قابل تعمیم به کل جمعیت نباشد. در این صورت تخمین های صورت گرفته اریب و متمایل به سمت یک زیر مجموعه ای باشد که گویای کل جمعیت نباشد.

در نتیجه مساله اصلی در نمونه برداری از گراف، الگوریتم و روش انتخاب نمونه‌ها و روش پیمایش گراف برای یافتن نمونه‌های بعدی است. سوالاتی که در این میان باید پاسخ داده شوند بدین قرار میباشند:

• چه راه‌کار نمونه برداری را مورد استفاده قرار دهیم؟
• اندازه گراف نمونه تا چه حد می‌تواند کوچک شود؟
• چگونه مقادیر بدست آمده برای گراف نمونه را به گراف بزرگ تعمیم دهیم؟

در هر صورت هدف اصلی ما در نمونه برداری گراف این است که ویژگیهای گراف نمونه تا حد امکان به گراف اصلی نزدیک باشد و یا بهتر است بگوییم ویژگیهای گراف اصلی به نحو دقیقتری قابل محاسبه از گراف فرعی باشد.

اهداف اصلی نمونه برداری گراف

در این میان ما باید به سوالاتی در این زمینه پاسخ دهیم: آیا میخواهیم گراف نمونه ویژگیهایی مانند گراف اصلی داشته باشد و یا میخواهیم گراف نمونه شبیه زمانی باشد که گراف اصلی به صورت کنونی رشد نکرده بود و اندازه گراف نمونه بود ؟ در حقیقت باید به این سوال پاسخ دهیم که میخواهیم هدف کوچک کردن گراف (Scale-down goal) را دنبال کنیم و یا بازگشت در زمان (Back-in-time goal) را.

Scale-down goal : در روش نمونه برداری با هدف کوچک کردن گراف، یک گراف بزرگ ایستایG  با n  نود در اختیار ما گذاشته شده و اندازه نهایی گراف نمونه نیز به ما داده شده است. هدف آن است که یک نمونه از گراف با نام S  و با تعداد n’ نود تولید کنیم به گونه‌ای که n’  خیلی کوچکتر از n باشد و گراف S نیز تا حد امکان از نظر ویژگیهای مختلف به گراف G  شبیه باشد. مثلا دارای توزیع درجه مشابه، فواصل نودهای مشابه، یا ساختار انجمنهای مشابه و … باشد. شباهت ویژگی ها در بخشهای بعدی به صورت فرمال معرفی خواهد شد.

Back-in-time goal: روش نمونه برداری با هدف بازگشت در زمان بدین معناست که مایلیم نسخه رشد نکرده و کوچک گراف G  را بدست آوریم. ما در این میان دیدی از درجه نودها و یالها نداریم اما میخواهیم گراف ساخته شده دقیقا به زمانی از تکامل گراف G  شبیه باشد که n’  نود داشته است. یعنی ميخواهيم یک گراف S  با n’ نود بیابیم که بیشترین شباهت را با گراف G داشته باشد، زمانی که دقیقا به اندازهS  دارای n’ نود بود.

در هر حال هدف از نمونه برداری، کوچک کردن گراف تا حد امکان است به گونه ای که ویژگی های گراف حفظ شده ولی پردازش و حافظه کمتری لازم داشته باشد. در نتیجه ما بر روی این هدف تمرکز خواهیم نمود.

تکنیکهای ارزیابی در نمونه برداری گراف

مساله بعد، لیستی از خصوصیات گراف اولیه است که میخواهیم در گراف نمونه آن ویژگی‌ها را حفظ کنیم. هدف ما در اینجا این نیست که  یک روش مدل سازی بیابیم که تنها یکی از خصوصیات گراف را حفظ کند ما به دنبال این هستیم که یک روش جامع و مانع برای مدل سازی پیدا کنیم که با تمامی خصوصیات گراف مطابقت کند تا در نتیجه گرافهای نمونه را بتوان به عنوان نمونه ای از مدل های پیچیده و هزینه‌بر استفاده کرد.

معیارهای ارزیابی یک گراف ایستا

گراف ایستا گرافی است که در طول زمان تغییر نمیکند یا تغییرات آن ناچیز شمرده میشود. گرافها معمولا تغییر دارند و در طول زمان تغییر میکنند. اما در یک بازه زمانی کوتاه مدت میتوان آنها را ایستا فرض کرد. پس اگر یک تصویر (snapshot) مربوطه به زمان خاصی از تکامل گراف موجود باشد میتوان به دیده گراف ایستا به آن نگاه کرد. حال با فرض داشتن یک تصویر ایستا از گراف میتوانیم ویژگی های زیر را روی آن محاسبه کرده و برای مقایسه گراف و نمونه برداشته شده از آن استفاده کنیم:

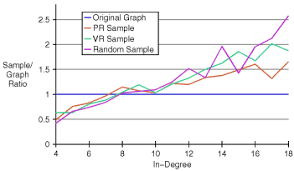
1. توزیع درجه ورودی نودها (In-Degree Ditribution): برای این معیار هیستوگرام درجه ورودی نودها، یعنی درصد نودهایی که درجه ورودی خاصی دارند را شمارش میکنیم. توزیع درجه شبکه های اجتماعی معمولا از توزیع توانی (power law) تبعیت میکند.
2. توزیع درجه خروجی (Out-degree): مشابه توزیع درجه ورودی با این تفاوت که بجای درجه ورودی شمارش بر روی درجه خروجی نودها انجام میگیرد.
3. توزيع تعداد اجزای دارای همبندی ضعیف گراف (Weakly connected components) : دو نود در صورتی با ارتباط ضعیف به هم وصل شده اند که بین این دو نود حداقل یک مسیر چه از نود اول به دوم چه بالعکس وجود داشته باشد.
4. توزیع تعداد اجزای قویا همبند گراف (Strongly connected components): اجزای قویا مرتبط زیر مجموعه ای از اجزای دارای همبندی ضعیف هستند که بین هر دو نود هم مسیری از نود اول به دوم و هم مسیری از نود دوم به اول وجود داشته باشد. توجه داشته باشیم که اجزای دارای همبندی قوی حتما دارای همبندی ضعیف هستند اما عکس آن برقرار نیست.
5. Hop-Plot: توزیع تعداد نودهایی که در h گام به همدیگر دسترسی دارند.
6. Hop-Plot روی بزرگترین جزء دارای همبندی ضعیف
7. توزیع اولین بردار تکینه سمت چپ ماتریس مجاورت نسبت به رتبه
8. توزیع مقادیر ویژه ماتریس مجاورت نسبت به رتبه که معمولا دارای توزیع دم پهن (heavy-tail) است.
9. توزیع ضریب خوشه بندی[9] گراف. ضریب خوشه بندی، یک کسر است و عبارت است از تعداد لینکهای موجود میان دوستان یک نود تقسیم بر تعداد لینکهای ممکن.

معیارهای ارزیابی تکامل زمانی گراف

وقتی که تصاویر مختلفی از تکامل یک گراف در طول زمان داشته باشیم علاوه بر این که معیارهای فوق را میتوانیم روی هر تصویر محاسبه و با هم مقایسه کنیم الگوی تغییر برخی ویژگی ها در طول زمان نیز امکان پذیر میشود. برای انجام این مقایسه، ما اصولا یک عدد اسکالر (مانند قطر گراف) را برای هر تصویر محاسبه کرده و بررسی کنیم این عدد با افزایش اندازه گراف چه تغییراتی کرده است.

معیارهای مقایسه تکامل زمانی گرافها به قرار زیر میباشد:

1. Densification Power law: نسبت تعداد یالها روی تعداد نودها در طول زمان. این قانون ادعا میکند که e(t) یعنی تعداد یالها در زمان t دارای توزیعی متناسب با n(t)^a است که n(t) تعداد نودها در زمان t است. توان a معمولا بزرگتر از یک است و این یعنی این که متوسط درجه نودها در طول زمان افزایش پیدا میکند.
2. قطر موثر گراف در طول زمان، که عبارت است از حداقل تعداد گامی است که 90 درصد از نودهای گراف بتوانند در گامهایی کمتر یا مساوی آن تعداد گام به یکدیگر دسترسی داشته باشند. مشاهده شده که قطر موثر در طول زمان کاهش می یابد و یا ثابت میماند.
3. تغییرات اندازه نرمالیزه شده بزرگترین جزء همبند گراف در طول زمان: که عبارت است از تعداد نودهای موجود در بزرگترین جزء همبند تقسیم بر تعداد کل نودها.
4. بزرگترین مقدار تکینه (singular value) ماتریس مجاورت گراف در طول زمان
5. میانگین ضریب خوشه‌بندی نودها در طول زمان.

دسته بندی الگوریتم های نمونه برداری گراف

الگوریتم های نمونه برداری گراف را میتوان به سه دسته تقسیم کرد:

• روشهای مبتنی بر انتخاب تصادفی نود ها
• روشهای مبتنی بر انتخاب تصادفی یالها
• روشهای مبتنی بر جستجوی تصادفی (exploration).

 

آدرس کانال تلگرام سایت بیگ دیتا:

t.me/bigdata_channel

آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel

جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.

جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.

 

بازدیدها: 1729