گرافچی (GraphChi) روشی برای پردازش و تحلیل گراف های بزرگ بر روی یک کامپیوتر است. این پروژه با سه زبان C, java و Scala بازنویسی شده است. که پروژه اصلی به زبان C است.

سیستم های امروزی محاسبات بر روی گراف برای برخورد با  مسائل واقعی (Real World Problems)، نیاز به یک خوشه محاسبتی توزیع شده (Distributed Computing Cluster) دارند. مانند محاسبات بر روی شبکه های اجتماعی یا گراف وب. با وجود اینکه در حال حاضر منابع محاسباتی توزیع شده بیشتر در دسترس هستند؛ ولی تولید الگوریتم های توزیع شده محاسباتی گراف هنوز هم مسئاله ای چالش برانگیز است. به همین منظور در این گزارش قصد داریم به معرفی و آزمایش Graphchi[1] که یک سیستم مبتنی بر دیسک(SSD یا Hard Disk) برای محاسبات گراف با میلیارد ها لبه (Edge) به صورت کارا است بپردازیم. Graphchi با خرد کردن گراف به بخش های کوچکتر و با استفاده از یک پنجره لغزان موازی (Parallel Sliding Window) خاص می تواند بسیاری از الگوریتم های پیشرفته داده کاوی و گراف کاوی، یادگیری ماشین را بر روی گراف های خیلی بزرگ و صرفاً توسط یک کامپیوتر معمولی اجرا کند. البته Graphchi طوری طراحی شده است که گراف های پویا را نیز که در طول زمان تغییر می کنند پشتیبانی می کند. برنامه های Graphchi همانند GraphLab[2] از مدل Vetrex-Centric نوشته شده اند.  در ادامه نشان خواهیم که Graphchi در عمل چه نقاط قوت و ضعفی دارد.

Graphchi  یک نرم افزار آنالیز و تجسم سازی شبکه های اجتماعی است که می تواند محاسبات بزرگ را روی یک ماشین با استفاده از یک الگوریتم جدید کشویی برای پردازش گراف از دیسک را داشته باشد. این نرم افزار در مدل راس محور بوده و برنامه های راس محور آسنکرون را اجرا می کند. این نرم افزار با نرم افزار Giraph Apachi مقایسه شده است. که نرم افزار  Giraph Apachi پنج میلیارد لبه را در حدود 75 دقیقه با Hadoop اجرا کرده در صورتی که گرافچی (GraphChi) همین کار مشابه را تقریبا در همان زمان تنها با یک ماشین انجام میدهد.

برخی از ویژگی های گرافچی (GraphChi) شامل موارد زیر است:

به روز رسانی جریان گراف و حذف لبه از گراف را پشتیبانی میکند

اجرای الگوریتم CF

مقیاس پذیری خطی

توانایی اجرای میلیارد ها لبه با یک لپ تاپ مدرن

هدف ایجاد این نرم افزار برای کارهای تجاری و دانشجویی بوده است و در سال 2010 انتشار پیدا کرده است

 

اصل منبع مبحث گرافچی (GraphChi) در زیر آورده شده در صورتی که فرصتی پیش بیاد در هفته های آینده ترجمه خواهم کرد.

Parallel Sliding Windows

This section describes the Parallel Sliding Windows (PSW) method (Algorithm 2). PSW can process a graph with mutable edge values efficiently from disk, with only a small number of non-sequential disk accesses, while supporting the asynchronous model of computation. PSW processes graphs in three stages: it 1) loads the graph from disk; 2) updates the vertices and edges; and 3) writes updated values to disk. These stages are explained in detail below, with a concrete example. We then present an extension to graphs that evolve over time, and analyze the I/O costs of the method.

Loading the Graph

Under the PSW method, the vertices V of graph G = (V, E) are split into P disjoint intervals. For each interval, we associate a shard, which stores all the edges that have destination in the interval. Edges are stored in the order of their source . Intervals are chosen to balance the number of edges in each shard; the number of intervals, P , is chosen so that any one shard can be loaded completely into memory. Similar data layout for sparse graphs was used previously, for example, to implement I/O efficient Pagerank and SpMV .

PSW does graph computation in execution intervals, by processing vertices one interval a time. To create subgraph of the vertices in interval p , edges (with their associated values) must be loaded from disk. First, Shard(p), which contains the in-edges for the vertices in interval(p), is loaded fully into memory. We call thus shard(p) the memory-shard. Second, because the edges are ordered by their source, the out-edges for the vertices are stored in consecutive chunks in the other shards, requiring additional P-1 block reads. Importantly, edges for interval(p+1) are stored immediately after the edges for interval(p). Intuitively, when PSW moves from an iteration to the next, it slides a window over each shard. We call the other shards the sliding shards. Note, that if the degree distribution of a graph is not uniform, the window length is variable. In total, PSW requires only P sequential disk reads to process each interval. A high-level illustration of the process is given in Figure , and the pseudo-code of the subgraph loading is provided in Algorithm 3.

Parallel Updates

After the subgraph for interval p has been fully loaded from disk, PSW executes the user-defined update-function for each vertex in parallel. As update-functions can modify the edge values, to prevent adjacent vertices from accessing edges concurrently (race conditions), we enforce external determinism, which guarantees that each execution of PSW produces exactly the same result. This guarantee is straight-forward to implement: vertices that have edges with both end-points in the same interval are flagged as critical, and are updated in sequential order. Non-critical vertices do not share edges with other vertices in the interval, and can be updated safely in parallel. Note, that the update of a critical vertex will observe changes in edges done by preceding updates, adhering to the asynchronous model of computation. This solution, of course, limits the amount of effective parallelism. For some algorithms, consistency is not critical (for example, see ), and we allow user to enable fully parallel updates.

Updating Graph to Disk

Finally, the updated edge values need to be written to disk and be visible to the next execution interval. PSW can do this efficiently: The edges are loaded from disk in large blocks, which are cached in memory. When the subgraph for an interval is created, the edges are referenced as pointers to the cached blocks. That is, modifications to edge values directly modify the data blocks themselves. After finishing the updates for the execution interval, PSW writes the modified blocks back to disk, replacing the old data. The memory-shard is completely rewritten, while only the active sliding window of each sliding shard is rewritten to disk (see Algorithm \ref{alg:PSW}). When PSW moves to next interval, it reads the new values from disk, thus implementing the asynchronous model. The number of non-sequential disk writes for a execution interval is $P$, exactly same as the number of reads. Note, if an algorithm only updates edges in one direction, PSW only writes the modified blocks to disk.

Simple Example

We now describe a simple example, consisting of two execution intervals, based on Figure below. In this example, we have a graph of six vertices, which have been divided into three equal intervals: 1-2, 3-4, and 5-6.

Figure a shows the initial contents of the three shards. PSW begins by executing interval 1, and loads the subgraph containing of edges drawn in bold in the figure c. The first shard is the memory-shard, and it is loaded fully. Memory-shard contains all in-edges for vertices 1 and 2, and a subset of the out-edges. Shards 2 and 3 are the sliding shards, and the windows start from the beginning of the shards. Shard 2 contains two out-edges of vertices 1 and 2; shard 3 has only one. Loaded blocks are shaded in Figure a.
After loading the graph into memory, PSW runs the update-function for vertices 1 and 2. After executing the updates, the modified blocks are written to disk; updated values can be seen in Figure b.

PSW then moves to second interval, with vertices 3 and 4. Figure d shows the corresponding edges in bold, and Figure b shows the loaded blocks in shaded color. Now shard 2 is the memory-shard. For shard 3, we can see that the blocks for the second interval appear immediately after the blocks loaded in the first. Thus, PSW just “slides” a window forward in the shard.

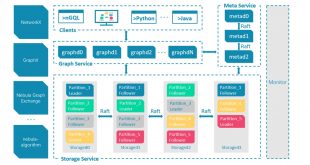
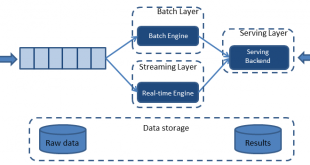
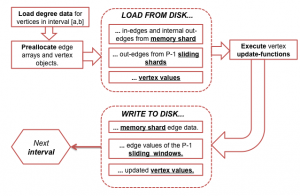
Operation Diagram

Diagram below shows the GraphChi operation flow.

Evolving Graphs and Streaming Graph Updates

See separate page for Evolving-And-Streaming-Graphs.

Compressed shards

Since version 0.2, GraphChi now stores the shards in 4-megabyte compressed blocks. This enables also DynamicEdgeData support. See more from GraphChi-Version0p2-Release.

https://github.com/GraphChi/graphchi-cpp/wiki/Introduction-To-GraphChi

[1] Graph Computing

[2] http://graphlab.org

آدرس کانال تلگرام سایت بیگ دیتا:

t.me/bigdata_channel

آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel

جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.

بازدیدها: 4143