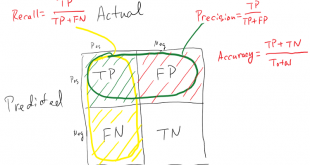
الگوریتم های برتر در حوزه داده کاوی، علم داده و یادگیری ماشین (قسمت اول)
مقدمه بر الگوریتم های برتر داده کاوی
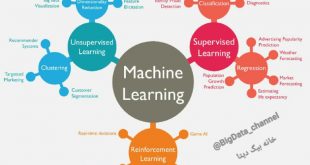
استفاده از دادهها به منظور کشف رابطه بین آنها اساس دادهکاوی است. در این مبحث 10 الگوریتم های داده کاوی و یادگیری ماشین که بیشترین کاربرد را در علم داده دارند را به صورت خلاصه آموزش میدهیم. که شامل موارد زیر می باشد: که البته پنج الگوریتم را در این قست و باقی الگوریتم ها را در قسمت های بعد بررسی می کنیم.
- رگرسیون خطی
- رگرسیون لجستیک
- خوشه بندی k-means
- پی سی ای(PCA)
- ساپوریت وکتور ماشین(SVM)
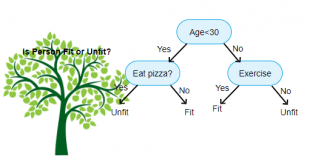
- درخت تصمیم
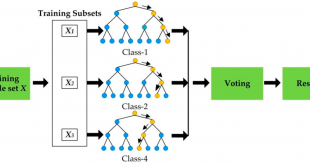
- جنگل تصادفی
- گرادینت بوستینگ ماشین
- ایکس جبوست
- شبکه عصبی

ولی قبل از شروع یادگیری الگوریتم ها داده کاوی واجب است یازده نکته طلایی درمورد علم داده که دانستن آن برای همه بسیار لازم است را بدانید.
?@BigData_channel
- هیچ وقت داده تمیز و آماده پردازش نیستند.
- شما باید عمده زمان را صرف پاکسازی داده و پیش پردازش کنید.
- هیچ روش تمام اتوماتیکی برای تحلیل داده وجود نداره و خودتان باید مستقیم با داده سر و کله بزنید.
- ۹۵ درصد تحلیل ها نیاز به روش یادگیری عمیق ندارند. پس خودتان را درگیر الگوریتم پیچیده نکنید.
- در عمل بیگ دیتا فقط ابزار است و ربطی به حجم داده ندارد.
- شما باید از رویکرد های بیزین استقبال کنید.
- هیچ کس، آنچه شما انجام داده اید را تضمین نمیکند.
- دنیای آکادمیک با دنیای کار عملیاتی دو جهان متفاوت هستند.
- نحوه ارائه خروجی ها یک مبحث کلیدی است.
- تمامی مدل ها خطا دارند. با این حال بعضی از آنها مفید هستند.
- درست هست که مدل های تحلیل قدرتمند هستند ولی این به این معنی نیست که میتوانید به واسطه آن نور را در روز مشاهده کنید.
عناوين مطالب: '
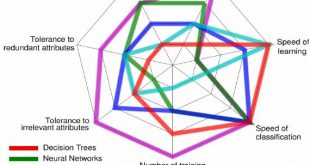
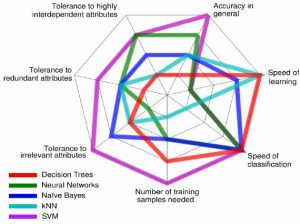
مقايسه اي بر الگوريتم هاي يادگيري ماشين از لحاظ کارايي
1- رگرسیون خطی
واژه رگرسیون برای اولین بار در مقاله معروف فرانسیس گالتون دیده شد که در مورد قد فرزندان و والدینشان بود. این واژه به معنی بازگشت است. او در مقاله خود در سال ۱۸۷۷ اشاره میکند که قد فرزندان قد بلند به میانگین قد جامعه میل میکند. او این رابطه را «بازگشت» (Regress) نامید.
در آمار، رگرسیون خطی یک رویکرد مدل خطی بین متغیر وابسطه(پاسخ) با یک یا چند متغیر مستقل(توصیف) است. اغلب برای کشف مدل رابطهی خطی بین متغیرها از رگرسیون (Regression) استفاده میشود.
برای سنجش شدت رابطه بین متغیر وابسته و مستقل میتوان از ضریب همبستگی استفاده کرد. هر چه ضریب همبستگی به ۱ یا ۱- نزدیکتر باشد، شدت رابطه خطی بین متغیرهای مستقل و وابسته شدیدتر است. البته اگر ضریب همبستگی نزدیک به ۱ باشد جهت تغییرات هر دو متغیر یکسان است که به آن رابطه مستقیم میگوییم و اگر ضریب همبستگی به ۱- نزدیک باشد، جهت تغییرات متغیرها معکوس یکدیگر خواهد بود و به آن رابطه عکس میگوییم. ولی در هر دو حالت امکان پیشبینی مقدار متغیر وابسته برحسب متغیر مستقل وجود دارد.
نمایش رابطهی خطی بین دو متغیر مستقل و وابسته معمولا توسط «نمودار نقطهای» (Scatter Plot) انجام میشود.
سادهترین مدل رگرسیونی، رگرسیون خطی است که شامل دو نوع خطی ساده و خطی چندگانه میباشد. مدلهای رگرسیونی خطی یک چارچوب وسیع و غنی را در بر میگیرند که نیاز تحلیلهای زیادی را برآورده میکند و پاسخ میدهد.
اما رگرسیون خطی برای همه مسائل نمیتواند مناسب باشد، زیرا بعضی از اوقات متغیر پاسخ و متغیرهای رگرسیونی با تابع غیرخطی معلوم به هم مربوط میشوند. مانند زمانی که متغیر وابسته ما دو سطح داشته باشد. یعنی پاسخها تنها شامل دو حالت، مانند وجود یا عدم وجود، خرید یا عدم خرید، بهبود یا عدم بهبود و… (که آنها را با مقادیر 0 و 1 نشان می دهیم) است.
در این مواقع از رگرسیون لجستیک استفاده میکنیم.
رگرسیون خطی چیست؟
در این قسمت رگرسیون خطی ساده و چندگانه مورد بررسی قرار میگیرد. در رگرسیون خطی ساده فقط یک متغیر پیشبینی کننده داریم. در حالی که در رگرسیون خطی چندگانه بیش از یک متغیر پیشبینی کننده داریم.
به عنوان مثال وقتی میخواهیم بررسی کنیم که آیا میزان ضریب هوشی دانشآموزان بر معدل آنها تاثیرگذار هست یا نه؟ از رگرسیون خطی ساده استفاده میکنیم. اما زمانی که میخواهیم بررسی کنیم، آیا میزان ضریب هوشی و ساعت مطالعه در هفته دانشآموزان بر معدل آنها تاثیرگذار هست یا نه؟ از رگرسیون خطی چندگانه استفاده میکنیم. در حالت اول برای پیشبینی متغیر پاسخ تنها یه متغیر مستقل داریم اما در حالت دوم برای پیشبینی متغیر پاسخ دو متغیر ضریب هوشی و ساعت مطالعه در هفته را داریم.
رگرسیون خطی ساده
قبل از انجام رگرسیون خطی ساده، قدم اول بررسی رابطه بین دو متغیر است. برای بررسی این رابطه نمودار پراکندگی بین دو متغیر را رسم میکنیم. یکی از سادهترین روشها برای بررسی هبستگی و رابطه بین متغیرها با یکدیگر رسم نمودار پراکندگی است.
ا بررسی این نمودار، خطی یا غیر خطی و مثبت یا منفی بودن رابطه بین دو متغیر را متوجه میشویم. همچنین با رسم نمودار پراکندگی میتوانیم نقاط پرت را نیز شناسایی کنیم. در رسم نمودار پراکندگی، متغیر مستقل یا پیشگو در محور افقی و متغیر وابسته یا پاسخ در محور عمودی قرار میگیرد.
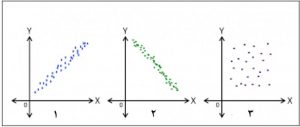
همانطور که در شکل 1 و 2 میبینید، نقاط حول یک خط راست جمع شدهاند پس در این دو شکل وجودرابطه خطی بین دو متغیر مشهود است. در شکل 1 رابطه خطی مثبت مشاهده میشود و در شکل 2 به دلیل اینکه شیب خط منفی است پس رابطه منفی دیده میشود. اما در شکل 3 رابطه خطی بین دو متغیر مشاهده نمیشود.
اگر رابطه خطی بین دو متغیر وجود نداشته باشد، مقدار ضریب همبستگی نزدیک صفر خواهد بود. اما ضریب همبستگی صفر به این معنی نیست که هیچ نوع رابطه بین دو متغیر وجود ندارد. بلکه ممکن است یک رابطه غیرخطی بین دو متغیر وجود داشته باشد. در رگرسیون خطی ساده متغیر وابسته یا پاسخ را با Y و متغیر مستقل یا پیشگو را با X نشان میدهیم و معادله خط رگرسیون ساده به صورت Y=aX+b است.
2- رگرسیون لجستیک (Logistic Regression)
یکی از روشهای «دستهبندی» (Classification) در مبحث «آموزش نظارت شده» (Supervised Machine Learning) رگرسیون لجستیک است. در این روش رگرسیونی، از مفهوم و شیوه محاسبه «نسبت بخت» (Odds Ratio) استفاده میشود.
رگرسیون خطی برای همه مسائل نمیتواند مناسب باشد، زیرا بعضی از اوقات متغیر پاسخ و متغیرهای رگرسیونی با تابع غیرخطی معلوم به هم مربوط میشوند. مانند زمانی که متغیر وابسته ما دو سطح داشته باشد. یعنی پاسخها تنها شامل دو حالت، مانند وجود یا عدم وجود، خرید یا عدم خرید، بهبود یا عدم بهبود و… (که آنها را با مقادیر 0 و 1 نشان می دهیم) است.
در این مواقع از رگرسیون لجستیک استفاده میکنیم. الگوهای رگرسیون لجستیک برای بیان پیشبینی متغیرهای دو حالتی الگوهای مناسبی هستند.این روش در ابتدا در کاربردهای پزشکی و برای احتمال وقوع یک بیماری مورد استفاده قرار میگرفت. لیکن امروزه در تمام زمینههای علمی کاربرد وسیعی یافته است. به عنوان مثال مدیر تبلیغاتی میخواهد بداند در خرید یا عدم خرید یک محصول یا برند، چه متغیرهایی مهم هستند؟
غیر از رگرسیون لجستیک انواع دیگری از مدلهای رگرسیون غیرخطی نیز وجود دارند که شامل: مدلهای توانی، معکوس، لگاریتمی، سهمی، نمایی، مرکب، رشد، منحنی S و … است.
رگرسیون لجستیک زمانی استفاده می شود که متغیر وابسته به صورت گروه بندی شده باشد.
متغیر وابسته می تواند ذاتا طبقه بندی شده باشد، بعنوان مثال :
- آیا یک ایمیل اسپم است (1) یا اسپم نیست (0)
- آیا یک تومور بدخیم است (1) یا خوش خیم (0)
متغیر وابسته می تواند ذاتا هم طبقه بندی شده نباشد و دارای مقیاس کمی فاصله ای یا نسبی باشد و خود محقق با توجه به سوال پژوهشی تحقیق، با در نظر گرفتن نقطه برش متغیر کمی موجود را به متغیر طبقه بندی شده تبدیل نماید و از رگرسیون لجستیک استفاده کند. بعنوان مثال:
- آیا یک فرد چاق است (1) یا در وضعیت نرمال و یا کمی اضافه وزن قرارد دارد (0). مشخص است که وضعیت چاقی فرد با شاخص BMI سنجیده می شود و اگر شخصی شاخص BMI بیشتر از 30 داشته باشد آن شخص چاق می باشد. در واقع می توان از مدل رگرسیون لجستیک برای طبقه بندی وضعیت چاقی یک فرد استفاده کرد، واضح است که متغیر BMI یک متغیر کمی فاصله ای می باشد که ما با در نظر گرفتن نقطه برش 30≤BMI آنرا به یک متغیر گروه بندی شده تبدیل کردیم (افرادی با 30>BMI در گروه افرادی با وضعیت نرمال و کمی اضافه وزن داشته باشند و افرادی که 30≤BMI دارند در گروه چاق قرار بگیرند).
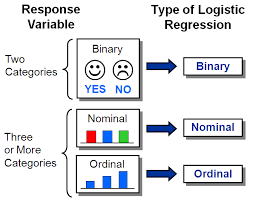
انواع رگرسیون لجستیک
- رگرسیون لجستیک باینری یا دو وجهی (Binary logistic regression)
- رگرسیون لجستیک چند سطحی یا چند وجهی (Multinomial logistic regression)
- رگرسیون لجستیک ترتیبی (Ordinal logistic regression)
3- خوشهبندی k-میانگین
الگوریتم k-میانگین یکی از سادهترین و محبوبترین الگوریتمهایی است که در «دادهکاوی» (Data Mining) بخصوص در حوزه «یادگیری نظارت نشده» (Unsupervised Learning) به کار میرود. الگوریتم خوشهبندی k-میانگین از گروه روشهای خوشهبندی تفکیکی (Partitioning Clustering) محسوب میشود.
الگوریتم خوشه بندی K-means به محاسبه نقاط مرکزی می پردازد و این کار را تکرار می کند تا نقطه مرکزی بهینه را پیدا کند. این الگوریتم فرض می کند که تعداد خوشه ها مشخص شده است. همچنین به آن الگوریتم خوشه بندی flat نیز گفته می شود. تعداد خوشه های مشخص شده در داده توسط الگوریتم، با k در K-means نمایش داده می شوند.
در این الگوریتم، نقاط داده به گونه ای به یک خوشه تخصیص داده می شوند که مجموع مربع فاصله بین نقاط داده و نقطه مرکزی کمینه باشد. قابل درک است که هر چه تغییرات در خوشه ها کمتر باشد، نقاط داده مشابه تری را درون خوشه خواهیم داشت.
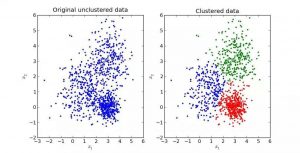
عملکرد الگوریتم K-Means :
در الگوریتم خوشهبندی K-Means ابتدا k عضو (که k تعداد خوشهها است) بصورت تصادفی از میان n عضو به عنوان مراکز خوشهها انتخاب میشود. سپس n-k عضو باقیمانده به نزدیکترین خوشه تخصیص مییابند. بعد از تخصیص همه اعضا مراکز خوشه مجدداً محاسبه میشوند و با توجه به مراکز جدید به خوشهها تخصیص مییابند و این کار تا زمانی که مراکز خوشهها ثابت بماند ادامه مییابد.
بهترین خوشهبندی آن است که مجموع تشابه بین مرکز خوشه و همه اعضای خوشه را حداکثر و مجموع تشابه بین مراکز خوشهها را حداقل کند. برای انتخاب بهترین خوشه ابتدا براساس نظرات خبره و مطالعات قبلی یک محدوده پیشنهادی برای تعداد خوشهها مشخص میشود. معمولاَ این محدوده بین انتخاب میشود. سپس مقدار ρ(k) برای هریک از مقادیر k محاسبه میشود. مقداری از k که در آن ρ(k) حداکثر شود، به عنوان تعداد بهینه خوشهها انتخاب میشود. به این ترتیب میتوان تعداد خوشهای را انتخاب نمود که به ازای آن فاصله بین مراکز خوشهها و شباهت مراکز خوشه با اعضای درون هر خوشه حداکثر است.
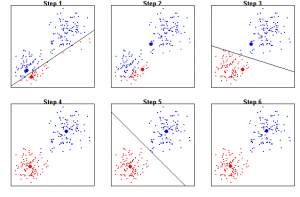
الگوریتم K-means از روش Expectation-Maximization برای حل مساله استفاده می کند. از مرحله انتظار (Expectation) برای تخصیص نقاط داده به نزدیکترین خوشه استفاده می شود و مرحله بیشینه سازی (Maximization) برای محاسبه نقطه مرکزی هر خوشه مورد استفاده قرار میگیرد.
در زمان کار با الگوریتم K-means، باید موارد زیر را در نظر داشته باشیم.
- در زمان کار با الگوریتم های خوشه بندی مانند K-means، توصیه می شود داده را به صورت استاندارد استفاده کنید، زیرا چنین الگوریتم هایی از اندازه گیری مبتنی بر فاصله برای تعیین شباهت بین نقاط داده استفاده می کنند.
- به علت ذات تکرار کننده K-Means و مقدار دهی اولیه نقاط مرکزی به صورت تصادفی، ممکن است K-Means به یک نقطه بهینه محلی برسد و به یک نقطه بهینه سراسری همگرا نشود.
برخی از ویژگی های مهم خوشه بندی K-Means :
• عملکرد الگوریتم وابسته به مراکز اولیه است
• اغلب در بهینەهای محلی خاتمه پیدا میکند
• خوشەها به شکلهای محدب هستند
• الگوریتمی موثر برای دادەهایی با حجم زیاد است(دلیل این ویژگی این است که پیچیدگی زمانی این الگوریتم O(nmkt) است که( n تعداد نمونه ها، m تعداد ویژگی ها، k تعداد خوشه ها و t تعداد تکرار است) و تابعی خطی از حجم نمونه میباشد.
برای روشن شدن موضوع به مثال زیر توجه کنید فرض کنید سن 9 نفر به صورت مجموعهی زیر جمع آوری شده است: {2, 4, 10, 12, 3, 20, 30, 11, 25} حال میخواهیم با استفاده از روش k-میانگین، دادههای به دست آمده را به دو خوشه تقسیم کنیم
گام 1 در این گام ابتدا باید دو عدد تصادفی به عنوان مراکز خوشهها تولید کنیم. فرض کنید اعداد 3 و 4 مراکز اولیه خوشه ها باشند .حال هریک از دادهها را با توجه به فاصله ی هریک از آنها از این مراکز، به یکی از خوشه ها نسبت میدهیم.به عنوان مثال عدد 2 به مرکز 3 و عدد 10 به مرکز4 نزدیکتر است.
بنابراین با ادامەی روند بالا، دو خوشەی زیر به دست میآیند ?1 = {2, 3} ?2 = {4, 10, 12, 20, 30, 11, 25}
گام ٢ (گام تکرار) در این گام مراکز جدید هر خوشه را محاسبه کرده و با توجه به مراکز جدید، دوباره عمل واگذاری دادهها را انجام میدهیم. که مراکز جدید 2.5 و 16خواهند بود.
مشاهده میشود عدد 4 که در مرحله قبل به خوشه دوم نسبت داده شد در این مرحله به مرکز خوشه اول نزدیکتر است. در نتیجه باید عدد 4 را در خوشه اول قرار دهیم. پس خوشه های جدید به شکل زیر خواهند بود: ?1 = {2, 3, 4} ?2 = {10, 12, 20, 30, 11, 25}
• روند بالا را تا زمانی ادامه میدهیم که شرط توقف برقرار شود
• مراحل بعدی به صورت زیر خواهند بود.
?1 = 3 ?2 = 18 → ?1 = {2, 3, 4, 10 } ?2 = {12, 20, 30, 11, 25}
مرحله بعد به صورت زیر خواهد بود
و مرحله نهایی به صورت زیر است که در ان مراکز ثابت شده است و خوشه ها تغییر نمیکنند.
4- آنالیز مولفه اصلی (Principal Component Analysis) یا PCA برای کاهش ابعاد
در این بخش از مطلب میخواهیم به یکی از مباحثِ اصلی و پیشرفتهتر در جبر خطی بپردازیم که به آن آنالیز مولفه اصلی (Principal Component Analysis) یا به اختصار PCA میگویند. که کاربرد آن را در مسائلِ حوزهی علومداده (Data Science) بسیار زیاد است.
یکی از کاربردهای اصلیِ PCA در عملیاتِ کاهشِ ویژگی (Dimensionality Reduction) است. PCA همانطور که از نامش پیداست میتواند مولفههای اصلی را شناسایی کند و به ما کمک میکند تا به جای اینکه تمامیِ ویژگیها را مورد بررسی قرار دهیم، یک سری ویژگیهایی را ارزشِ بیشتری دارند، تحلیل کنیم. در واقع PCA آن ویژگیهایی را که ارزش بیشتری فراهم میکنند برای ما استخراج میکند.
اجازه بدهید با یک مثال شروع کنیم. فرض کنید یک فروشگاه میخواهد ببیند که رفتار مشتریانش در خریدِ یک محصول خاص (مثلا یک کفش خاص) چطور بوده است. این فروشگاه، اطلاعات زیادی از هر فرد دارد (همان ویژگیهای آن فرد). برای مثال این فروشگاه، از هر مشتری ویژگیهای زیر را جمعآوری کرده است:
سن، قد، جنسیت، محل تولد شخص (غرب ایران، شمال ایران، شرق ایران یا جنوب ایران)، میانگین تعداد افراد خانواده، میانگین درآمد، اتومبیل شخصی دارد یا خیر و در نهایت اینکه این شخص بعد از بازدید کفش خریده است یا خیر. ۷ویژگیِ اول ابعاد مسئله ما را میساختند و ویژگیِ آخر هدف (Target) میباشد.
ویژگیهای بالا را میتوان برای مجموعهی داده (در اینجا مجموعه مشتریان فروشگاه) در ۷بُعد رسم کرد. حال به PCA بازمیگردیم. PCA میتواند آن مولفههایی را انتخاب کند که نقش مهمتری در خرید دارند. برای مثال، مدیرِ فروش به ما گفته است که به جای اینکه هر ۷بُعد را در تصمیمگیری دخالت دهیم، نیاز به ۳بُعد (۳ویژگی) داریم تا بتوانیم آنها را بر روی یک رابطِ گرافیکی ۳بُعدی به نمایش دربیاوریم. پس در واقع نیاز داریم ۷بُعد را به ۳بُعد کاهش دهیم. به این کار در اصطلاح کاهش ابعاد یا Dimensionality Reduction میگویند. PCA میتواند این کار را برای ما انجام دهد. PCA با توجه دادهها و دامنهی تغییراتِ هر کدام از آنها، میتواند ویژگیهایی را انتخاب کند که تاثیر حداکثری در نتیجه نهایی داشته باشند. در مثال بالا (فروشگاه)، فرض کنید ویژگی قد، تاثیر زیادی در اینکه یک فرد از فروشگاه خرید کند نداشته باشد. PCA این قضیه را متوجه میشود و در الگوریتمِ خود ویژگیِ قد را تا جای ممکن حذف میکند.
البته این بدان معنا نیست که در فرآیند کاهش ابعاد، PCA دقیقا همان ویژگی را حذف میکند. بلکه PCA توان این را دارد که به یک سری ویژگی جدید برسد. مثلا این الگوریتم ممکن است به این نتیجه برسد که افرادی که در شمال و غرب ایران زندگی میکنند و سنِ آنها بالای ۴۰سال است، احتمال خرید بالایی دارند در حالی که برعکس این قضیه احتمال خرید را بسیار کمتر میکند. در واقع اینجا PCA به یک ویژگی ترکیبی از محل تولد شخص و سن رسیده است. این دقیقا یکی از قدرتهای الگوریتم PCA در کار بر روی دادهها است.( تصویر زیر)
برای سادگی فرض کنید دادههای مشتریان ما کلا ۲بُعد دارند. سن و قد. حال (همانطور که در درس ویژگی چیست خواندید) آنها را بر روی محور مختصات نمایش میدهیم. هر کدام از نقاط آبی رنگ، در مثال ما یک مشتری است که با توجه به ویژگی سن (محور افقی) و ویژگی قد (محور عمودی) در صفحه مختصات رسم شده است. بردار ویژه میتواند کمک کند تا در میان دادههای ما خطی کشیده شود که بیشترین دامنه تغییرات در امتداد آن خط رخ داده باشد. ( تصویر زیر)
همانطور که گفتیم هر کدام از نقاط آبی رنگ، در مثالِ ما یک مشتری است که با توجه به ویژگی سن (محور افقی) و ویژگی قد (محور عمودی) در صفحه مختصات رسم شده است. فاصله هر نقطه آبی تا خط قرمز را میتوان به عنوان یک خطا (Error) در نظر گرفت و به تبعِ آن مجموعِ خطا برابر است با جمع فاصله تک تکِ نقاط آبی تا خط قرمز. به شکل زیر نگاه کنید، کدام تصویر (الف، ب یا ج) مجموع خطاهای کمتری دارند؟
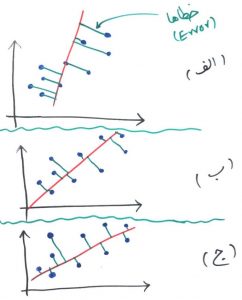
کمی دقت کنید. فاصله نقاط نسبت به خط قرمز با خط با رنگ سبز مشخص شدهاند. اگر جمع این فاصله (خطا – Error) را برای هر نمودار برابر خطای کلی دادهها نسبت به خط قرمز در نظر بگیریم، تصویرِ الف بیشترین میزان خطا را دارد و بعد از آن تصویر ب و در نهایت تصویر ج کمترین خطا را دارد. PCA به دنبال ساختنِ خطی مانند خط ج است(که در واقع همان بردار ویژه ماست و که کمترین خطا (Least Error) را داشته باشد.
در این مثال آخر ما ۲بُعد را به ۱بُعد کاهش دادیم. البته در مثالهای واقعی ممکن است ۱۰۰۰بُعد را به ۲بُعد کاهش دهند تا بتوان آن را بر روی یک نمودار به نمایش درآورد و این کار با با PCA انجام دهند که هم از سرعتِ معقولی برخوردار است و هم کیفیت قابل قبولی دارد.
منبع:مدرس: مسعود کاویانی سایت chistio.ir
چه زمانی باید از PCA استفاده کنیم؟
- آیا می خواهید تعداد متغیر ها را کاهش دهید، اما قادر به شناسایی متغیر ها برای حذف کامل از معادلات نیستید؟
- آیا می خواهید مطمئن شوید که متغیر ها مستقل از یکدیگر هستند؟
- آیا مایل هستید که متغیر های مستقل خود را کم تر تفسیر پذیر کنید؟
اگر پاسخ شما به هر سه سوال مثبت است، PCA روش خوبی برای استفاده است. اگر به سوال ۳ ” نه ” پاسخ دهید، نباید از PCA استفاده کنید
5- ماشین بردار پشتیبان یا SVM
«ماشین بردار پشتیبان» (SVM) یک الگوریتم نظارتشده یادگیری ماشین است که هم برای مسائل طبقهبندی و هم مسائل رگرسیون قابل استفاده است؛ با این حال از آن بیشتر در مسائل طبقهبندی استفاده میشود. در الگوریتم SVM، هر نمونه داده را به عنوان یک نقطه در فضای n-بعدی روی نمودار پراکندگی دادهها ترسیم کرده (n تعداد ویژگیهایی است که یک نمونه داده دارد) و مقدار هر ویژگی مربوط به دادهها، یکی از مؤلفههای مختصات نقطه روی نمودار را مشخص میکند. سپس، با ترسیم یک خط راست، دادههای مختلف و متمایز از یکدیگر را دستهبندی میکند.
برای توضیح کامل مسأله، فرض کنید دو پارامتری که قرار است جنسیت را از روی آنها تعیین کنیم، قد و طول موی افراد است . نمودار پراکنش قد و طول افراد در زیر نمایش داده شده است که در آن جنسیت افراد با دو نماد مربع (مرد) و دایره (زن) به طور جداگانه نمایش داده شده است .
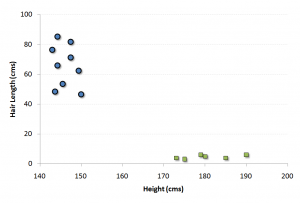
با نگاه به نمودار فوق، حقایق زیر به سادگی قابل مشاهده است :
- مردان در این مجموعه، میانگین قد بلندتری دارند.
- زنان از میانگین طول موی بیشتری برخوردار هستند.
اگر یک داده جدید با قد ۱۸۰cm و طول موی ۴cm به ما داده شود، بهترین حدس ما برای ماشینی این شخص، دسته مردان خواهد بود .
بردارهای پشتیبان و ماشین بردار پشتیبان
بردارهای پشتیبان به زبان ساده، مجموعه ای از نقاط در فضای n بعدی داده ها هستند که مرز دسته ها را مشخص می کنند و مرزبندی و دسته بندی داده ها براساس آنها انجام می شود و با جابجایی یکی از آنها، خروجی دسته بندی ممکن است تغییر کند. به عنوان مثال در شکل فوق ، بردار (۴۵,۱۵۰) عضوی از بردار پشتیبان و متعلق به یک زن است . در فضای دوبعدی ،بردارهای پشتیبان، یک خط، در فضای سه بعدی یک صفحه و در فضای n بعدی یک ابر صفحه را شکل خواهند داد.
در SVM فقط داده های قرار گرفته در بردارهای پشتیبان مبنای یادگیری ماشین و ساخت مدل قرار می گیرند و این الگوریتم به سایر نقاط داده حساس نیست و هدف آن هم یافتن بهترین مرز در بین داده هاست به گونه ای که بیشترین فاصله ممکن را از تمام دسته ها (بردارهای پشتیبان آنها) داشته باشد .
چگونه یک ماشین بر مبنای بردارهای پشتیبان ایجاد کنیم ؟
به ازای داده های موجود در مثال فوق، تعداد زیادی مرزبندی می توانیم داشته باشیم که سه تا از این مرزبندی ها در زیر نمایش داده شده است.
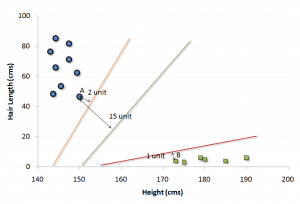
سوال اینجاست که بهترین مرزبندی در این مسأله کدام خط است ؟
یک راه ساده برای انجام اینکار و ساخت یک دسته بند بهینه ، محاسبه فاصله ی مرزهای به دست آمده با بردارهای پشتیبان هر دسته (مرزی ترین نقاط هر دسته یا کلاس) و در نهایت انتخاب مرزیست که از دسته های موجود، مجموعاً بیشترین فاصله را داشته باشد که در شکل فوق خط میانی ، تقریب خوبی از این مرز است که از هر دو دسته فاصله ی زیادی دارد. این عمل تعیین مرز و انتخاب خط بهینه (در حالت کلی ، ابر صفحه مرزی) به راحتی با انجام محاسبات ریاضی نه چندان پیچیده قابل پیاده سازی است .
توزیع غیر خطی داده ها و کاربرد ماشین بردار پشتیبان
اگر داده ها به صورت خطی قابل تفکیک باشند، الگوریتم فوق می تواند بهترین ماشین را برای تفکیک داده ها و تعیین دسته یک رکورد داده، ایجاد کند اما اگر داده ها به صورت خطی توزیع شده باشند (مانند شکل زیر )، SVM را چگونه تعیین کنیم ؟
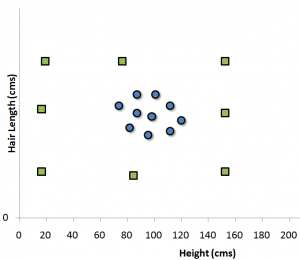
در این حالت، ما نیاز داریم داده ها را به کمک یک تابع ریاضی (Kernel functions) به یک فضای دیگر ببریم (نگاشت کنیم ) که در آن فضا، داده ها تفکیک پذیر باشند و بتوان SVM آنها را به راحتی تعیین کرد. تعیین درست این تابع نگاشت در عملکرد ماشین بردار پشتیبان موثر است که در ادامه به صورت مختصر به آن اشاره شده است.
با فرض یافتن تابع تبدیل برای مثال فوق، فضای داده ما به این حالت تبدیل خواهد شد :
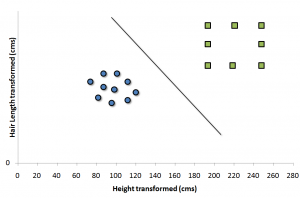
در این فضای تبدیل شده، یافتن یک SVM به راحتی امکان پذیر است .
نگاهی دقیق تر به فرآیند ساخت SVM
همانطور که اشاره شد،ماشین بردار پشتیبان یا SVM داده ها را با توجه به دسته های از پیش تعیین شده آنها به یک فضای جدید می برد به گونه ای که داده ها به صورت خطی (یا ابر صفحه ) قابل تفکیک و دسته بندی باشند و سپس با یافتن خطوط پشتیبان (صفحات پشتیبان در فضای چند بعدی) ، سعی در یافتن معادله خطی دارد که بیشترین فاصله را بین دو دسته ایجاد می کند.
در شکل زیر داده ها در دو دوسته آبی و قرمز نمایش داده شده اند و خطوط نقطه چین ، بردار های پشتیبان متناظر با هر دسته را نمایش می دهند که با دایره های دوخط مشخص شده اند و خط سیاه ممتد نیز همان SVM است . بردار های پشتیبان هم هر کدام یک فرمول مشخصه دارند که خط مرزی هر دسته را توصیف می کند.
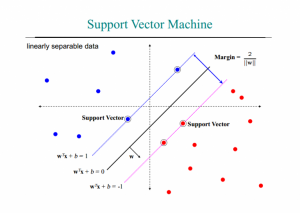
مزایا و معایب الگوریتم ماشین بردار پشتیبان
- مزایا
- حاشیه جداسازی برای دستههای مختلف کاملاً واضح است.
- در فضاهای با ابعاد بالاتر کارایی بیشتری دارد.
- در شرایطی که تعداد ابعاد بیش از تعداد نمونهها باشد نیز کار میکند.
- یک زیر مجموعه از نقاط تمرینی را در تابع تصمیمگیری استفاده میکند (که به آنها بردارهای پشتیبان گفته میشود)، بنابراین در مصرف حافظه نیز به صورت بهینه عمل میکند.
- معایب
- هنگامی که مجموعه دادهها بسیار بزرگ باشد، عملکرد خوبی ندارد، زیرا نیازمند زمان آموزش بسیار زیاد است.
- هنگامی که مجموعه داده نوفه (نویز) زیادی داشته باشد، عملکرد خوبی ندارد و کلاسهای هدف دچار همپوشانی میشوند.
- ماشین بردار پشتیبان به طور مستقیم تخمینهای احتمالاتی را فراهم نمیکند و این موارد با استفاده از یک اعتبارسنجی متقابل (Cross Validation) پرهزینه پنجگانه انجام میشوند. این امر با روش SVC موجود در کتابخانه scikit-kearn پایتون، مرتبط است.
منبع: bigdata.ir
آدرس کانال تلگرام سایت بیگ دیتا:
آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel
جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.
جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.
منابع:
http://www.bigdata.ir.
.https://chistio.ir/%D8%A2%D9%86%D8%A7%D9%84%DB%8C%D8%B2-%D9%85%D9%88%D9%84%D9%81%D9%87-%D8%A7%D8%B5%D9%84%DB%8C-principal-component-analysis-pca-%DA%86%DB%8C%D8%B3%D8%AA%D8%9F/
.http://www.tahlildadeh.com/ArticleDetails/k-means-Clustering
http://saeedansarifar.blog.ir/1399/05/29/%D8%B1%DA%AF%D8%B1%D8%B3%DB%8C%D9%88%D9%86-%D9%84%D8%AC%D8%B3%D8%AA%DB%8C%DA%A9-%D9%88-%D8%A7%D9%86%D9%88%D8%A7%D8%B9-%D8%A2%D9%86
.https://blog.faradars.org/simple-linear-regression/
.https://amarpishro.com/statistics-training/linear-regression/
بازدیدها: 3621
برچسبPCA SVM استخراج ویژگی الگوریتم های پر کاربرد الگوریتم های پرکاربرد در علم داده الگوریتم های داده کاوی انتخاب ویژگی بردار بردار ویژه داده کاوی رگرسیون خطی علم داده کاهش ابعاد گاهش ابعاد یادگیری ماشین
همچنین ببینید
دانلود مجموعه داده اخبار با طبقه بندی موضوعی (classification)
به منظور استفاده دانشجوبان عزیز در انجام پایان نامه حدود بیست هراز مجموعه داده اخبار …
مراحل پیشپردازش متن خبر فارسی
پیشپردازش متن فارسی برای پردازش زبان طبیعی و انجام عمليات خودکار بر روي متن مانند …
 خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم
خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم