نحوه تشخیص گراف دو بخشی و پیاده سازی آن

به منظور تایید گراف دو بخشی (که در مبحث تئوری گراف آموختیم) میخواهیم بررسی کنیم آیا میتوان رأس‌های گراف را به دو بخش افراز کرد به گونه‌ای که تمام یال‌ها بین این دو بخش بیافتد. بنابر قضیه‌های گراف، شرط دو‌بخشی بودن با دور فرد نداشتن متناظر است، پس کافیست این شرط را چک کنیم.
برای تست این شرط و افراز به دو مجموعه، میتوانیم از هر دو الگوریتم جست‌و‌جوی عمق‌اول و جست‌و‌جوی سطح‌اول استفاده کنیم. کافیست نحوه علامت گذاری مزاعفی در این دو الگوریتم را به گونه ای اضافه کنیم که از رأس‌های با رنگ ۰ به رأس‌های با رنگ ۱ برویم و برعکس. حال اگر به رأسی با علامت ۱ رسیدیم که همسایه‌ای از آن از قبل رنگ ۱ را داشت، پس در نتیجه دور فرد پیدا شده است و نمیتوان این کار را کرد؛ برای علامت ۰ نیز به همین ترتیب است. حال اگر هیچ یک از این دو حالت اتفاق نیافتد، در نتیجه میتوان این کار را کرد و رأس‌هایی که علامت ۱ را دارند در یک دسته و بقیه را در دسته مقابل قرار می‌دهیم.
دقت کنید که ممکن است گراف نا‌همبند باشد در نتیجه برای تمام رأس‌های دیده نشده این الگوریتم را تکرار میکنیم.
برای این کار از جست‌و‌جوی اول‌سطح (Breadth First Search) که به bfs مشهور است استفاده نموده ایم، روشی برای پیمایش گراف است که بعد از جست‌وجوی عمق‌اول مهم‌ترین و پرکاربرد‌ترین الگوریتم پیمایش گراف است. این الگوریتم معمولا در گراف‌ها‌ی وزن دار کاربرد خاصی ندارد و عمده نقش آن در گراف‌های بی‌وزن و برای پیدا کردن کوتاه‌ترین فاصله بین یک راس تا بقیه‌ی راس‌هااست.

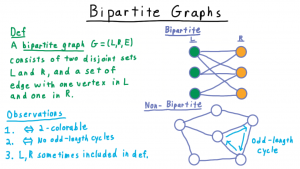
الگوریتم گراف دو بخشی
این الگوریتم ابتدا یک راس ریشه مانند v را به عنوان شروع میگیرد. سپس راس‌ها را سطح بندی میکند. سطح بندی به این صورت است که تمام راس‌های مجاور v را در سطح اول قرار میدهیم، حال برای سطح i+1
، راس u که مجاور یکی از رئوس سطح i است را در این سطح قرار میدهیم به شرطی که u در هیچ سطح دیگری نیامده باشد. به عبارت دیگر راس هارا بر اساس کوتاه‌ترین فاصله از v سطح بندی میکنیم. حال برای پیمایش به ترتیب سطح، و در هر سطح به ترتیب دلخواه وارد راس‌ها میشویم. پس اولین زمانی که به هر راس می‌رسیم، با کمترین فاصله ممکن نسبت به v رسیده ایم.
پیچیدگی‌ الگوریتم
با توجه به اینکه به هر راس حداکثر یکبار وارد میشویم در نتیجه هر یالی هم حداکثر دوبار به ازای دو سر آن شمرده می‌شود، پس در کل هزینه الگوریتم از O(n+e) است که e تعداد یال‌ها و n تعداد راس‌ها است.bi
پیاده‌سازی
برای ایجاد سطح های مختلف و حرکت به ترتیب سطح ها نیاز به استفاده از صف داریم.
فرض کرده ایم که لیست مجاورت راس ها را داده اند و الگوریتم راس آغازین را نیز از ورودی می‌گیرد.

 

1. import java.util.InputMismatchException;
2. import java.util.LinkedList;
3. import java.util.Queue;
4. import java.util.Scanner;
5.
6. public class BipartiteBfs
7. {
8. private int numberOfVertices;
9. private Queue queue;
10.
11. public static final int NO_COLOR = 0;
12. public static final int RED = 1;
13. public static final int BLUE = 2;
14.
15. public BipartiteBfs(int numberOfVertices)
16. {
17. this.numberOfVertices = numberOfVertices;
18. queue = new LinkedList();
19. }
20.
21. public boolean isBipartite(int adjacencyMatrix[][], int source)
22. {
23. int[] colored = new int[numberOfVertices + 1];
24. for (int vertex = 1; vertex <= numberOfVertices; vertex++)
25. {
26. colored[vertex] = NO_COLOR;
27. }
28. colored[source] = RED;
29. queue.add(source);
30.
31. int element, neighbour;
32. while (!queue.isEmpty())
33. {
34. element = queue.remove();
35. neighbour = 1;
36. while (neighbour <= numberOfVertices)
37. {
38. if (adjacencyMatrix[element][neighbour] == 1 && colored[element]== colored[neighbour])
39. {
40. return false;
41. }
42. if (adjacencyMatrix[element][neighbour] == 1 && colored[neighbour]== NO_COLOR)
43. {
44. colored[neighbour] = (colored[element] == RED ) ? BLUE :RED;
45. queue.add(neighbour);
46. }
47. neighbour++;
48. }
49. }
50. return true;
51. }
52.
53. public static void main(String... arg)
54. {
55. int number_of_nodes, source;
56. Scanner scanner = null;
57. try
58. {
59. System.out.println("Enter the number of nodes in the graph");
60. scanner = new Scanner(System.in);
61. number_of_nodes = scanner.nextInt();
62.
63. int adjacency_matrix[][] = new int[number_of_nodes + 1][number_of_nodes + 1];
64. System.out.println("Enter the adjacency matrix");
65. for (int i = 1; i <= number_of_nodes; i++)
66. {
67. for (int j = 1; j <= number_of_nodes; j++)
68. {
69. adjacency_matrix[i][j] = scanner.nextInt();
70. }
71. }
72.
73. for (int i = 1; i <= number_of_nodes; i++)
74. {
75. for (int j = 1; j <= number_of_nodes; j++)
76. {
77. if(adjacency_matrix[i][j] == 1 && adjacency_matrix[j][i] == 0)
78. {
79. adjacency_matrix[j][i] = 1;
80. }
81. }
82. }
83.
84. System.out.println("Enter the source for the graph");
85. source = scanner.nextInt();
86.
87. BipartiteBfs bipartiteBfs = new BipartiteBfs(number_of_nodes);
88. if (bipartiteBfs.isBipartite(adjacency_matrix, source))
89. {
90. System.out.println("The given graph is bipartite");
91. } else
92. {
93. System.out.println("The given graph is not bipartite");
94. }
95. } catch (InputMismatchException inputMismatch)
96. {
97. System.out.println("Wrong Input format");
98. }
99. scanner.close();
100. }
101. }

102. Enter the number of nodes in the graph
103. 4
104. Enter the adjacency matrix
105. 0 1 0 1
106. 1 0 1 0
107. 0 1 0 1
108. 1 0 1 0
109. Enter the source for the graph
110. 1
111. The given graph is bipartite

 

آدرس کانال تلگرام سایت بیگ دیتا:

t.me/bigdata_channel

آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel

جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.

منبع:

https://s3.amazonaws.com/content.udacity-data.com/courses/gt-cs6505/bipartitematching.html

بازدیدها: 2893