بررسی ساختار و توپولوژی گراف شبکه های اجتماعی
بررسی ساختار و توپولوژی گراف شبکه های اجتماعی
شبکههاي اجتماعي به طور عمده از دو ديدگاه قابل بررسي ميباشند: ساختار و ديناميک ( به زبان ساده داینامیک یعنی تحلیل در بستر زمان). بررسيها نشان ميدهد که اين شبکه ها در خصوصيات مشترک ساختاري به طرز قابل توجّهي اشتراک دارند. تحلیل های با ارزشی به منظور گراف کاوی تا کنون ارائه شده است. ولی معمولا چند دسته الگوریتم زیر بیشترین کاربرد ها را دارند.
1- الگوریتم های تشخیص مرکزیت
2- الگوریتم های تشخیص انجمن
3- الگوریتم های بصری سازی
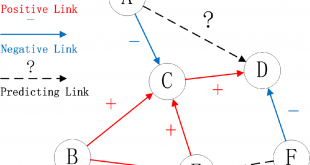
4- الگوریتم های پیشبینی ارتباطات
5- الگوریتم های نمومه برداری
در اين قسمت ابتدا به خصوصيات ساختاري که در سالهاي اخير و با توجّه به افزايش ميزان دادههاي قابل دسترسي در مورد شبکهها و نيز افزايش قدرت محاسباتي براي بررسي آنها کشف گرديده است، اشاره مينماييم. سپس به مدلهاي رياضياي که براي ايجاد گرافهايي با اين خصوصيات ساختاري پيشنهاد شدهاند خواهيم پرداخت. در بخش های ديگر به ويژگيهاي ديناميکي خواهيم پرداخت.
در دههي اخير، بررسي ساختار شبکهها با استفاده از دادههاي واقعي و ابزارهاي پردازشي قوي، خصوصيات مشابه انواع شبکهها با يکديگر را آشکار کرده است. به عنوان مثال کوچک بودن ميانگين کوتاهترين فاصلهها، بالا بودن خوشهبندي و وجود انجمنها در شبکههاي پيچيده تنها برخي از خصوصيات مشترک شبکهها در علوم مختلف ميباشد. حضور تمامي اين خصوصيات در شبکههاي واقعي آنان را از مدلهاي بررسي شده در رياضيات، مانند تورها (Lattice) و گرافهاي تصادفي(Random Graphs)، متمايز ميکند. اين خصوصيات موجب شده است که نحوهي شکلگيري تکاملي شبکههاي واقعي مورد بررسي دقيق قرار گيرد و مدلهايي براي ايجاد شبکههاي پيچيده با چنين ساختارهايي با الهام از نحوهي شکلگيري شبکههاي واقعي ارائه گردد.
توپولوژی شبکه های اجتماعی نقش مهمی در استخراج برخی اطلاعات از آنها ایفا میکند. توپولوژی شبکه به ساختار و نحوه اتصال نودهای آن اشاره دارد. قسمت اعظم فرایند استخراج توپولوژی شبکه با استفاده از توزیع درجه نودها انجام می شود.
امروزه با بررسي ساختار شبکهها با استفاده از دادههاي واقعي و ابزارهاي پردازشي قوي، خصوصيات مشابه انواع شبکهها با يکديگر را آشکار کرده است. به عنوان مثال کوچک بودن ميانگين کوتاهترين فاصلهها ، بالا بودن خوشهبندي و وجود انجمنها در شبکههاي پيچيده تنها برخي از خصوصيات مشترک شبکهها در علوم مختلف ميباشد. حضور تمامي اين خصوصيات در شبکههاي واقعي آنان را از مدلهاي بررسي شده در رياضيات، مانند تورها(Lattice) و گرافهاي تصادفي(Random Graphs)، متمايز ميکند. اين خصوصيات موجب شده است که نحوهي شکلگيري تکاملي شبکههاي واقعي مورد بررسي دقيق قرار گيرد و مدلهايي براي ايجاد شبکههاي پيچيده با چنين ساختارهايي با الهام از نحوهي شکلگيري شبکههاي واقعي ارائه گردد. برخی از مهم ترین خصوصیات ساختاری شبکه های اجتماعی در ذیل آمده است/
- توزیع فراوانی درجات گره ها(Degree distribute)
- ضریب کلوپ پولداران(Rich club)
- قطر گراف (Diameter)
- ضریب تراگذری (Transitivity coefficient )
- ضریب خوشه بندی(Clustering Coefficient)
- محاسبه کوتاهترین مسیر میان گرههای گراف
- فاصله متوسط گره ها از هم
همانطور که میبینید تنوع این معیارها و تعداد آنها بسیار زیاد است از همین رو ما به توضیح مهمترین و پرکاربردترین آنها اکتفا خواهیم کرد. معیارهای مورد بررسی ما در اینجا عبارتند از:
- خصوصیت استقلال از مقياس (به عبارتی توزیع فراوانی درجات گره ها)
درجه یک گره تعداد گره هایی است که با آن گره در همسایگی مستقیم قرار دارد.هر چقدر درجه یک گره بیشتر باشد، اهمیت آن گره بیشتر می شود.مثلا در شبکه وب، اگر درجه ورودی یک دامنه زیاد باشد، یعنی سایت مرجع است، و اگر درجه خروجی آن زیاد باشد، یعنی اینکه سایتی است که از اطلاعات (اخبار) سایت های دیگر استفاده می کند. توزیع درجات، توزیع احتمال این درجات روی کل شبکه است. توزیع درجات شبکه p(k) با استفاده از رابطه p(k)=n_k/n محاسبه می شود.
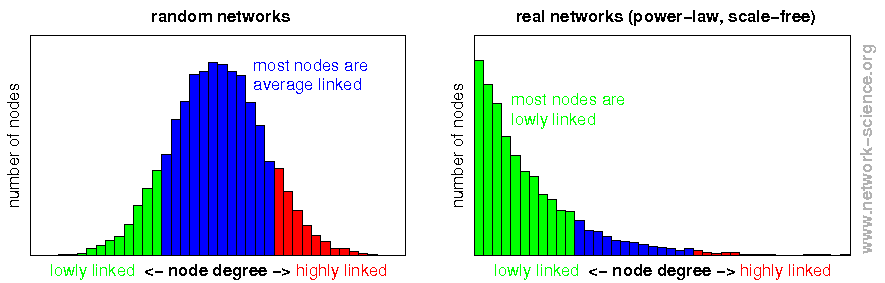
گرافهاي مورد بررسي در رياضيات عموماً از ساختار همگوني(Homogenous) مانند تورها و گرافهاي تصادفي برخوردارند. تا قبل از بررسي شبکههاي واقعي تصور بر اين بود که توزيع درجهي شبکههاي واقعي مانند اينگونه گرافها پوآسن باشد. امّا با بررسي بيشتر روشن شد که توزيع درجه در اکثريت قريب به اتّفاق شبکههاي واقعي از توزيع “قانون توانی (Power Law)” تبعيت ميکند. همانطور که مشاهده میشود تعداد گرههایی با درجه بالا کم و تعداد گرههایی با درجه کم زیاد است و این توزیع را میتوان با یک توزیع توانی تخمین زد. ترسیم نمودار log-log این گراف یک خط راست را نشان میدهد.
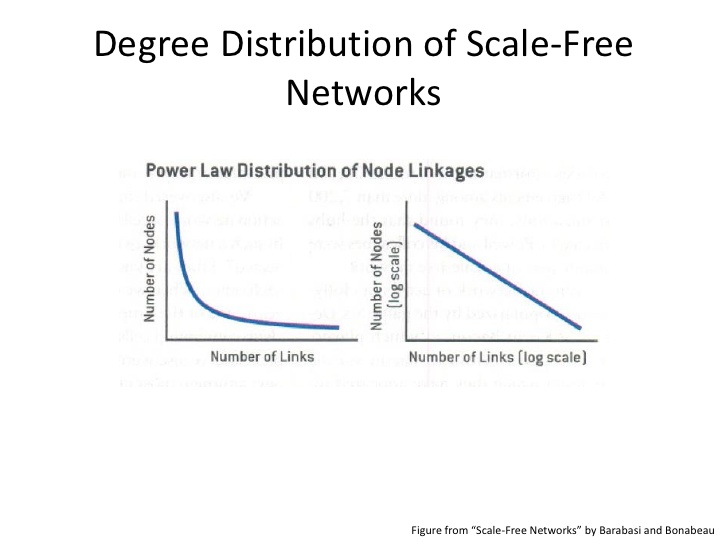
به اينگونه شبکهها، شبکههاي “مستقل از مقياس(Scale Free)” ميگويند. چرا که اين توزيع درجه تنها توزيع درجهاي است که در صورت بزرگ و کوچک شدن مقياس (به غير از اضافه شدن يک ضريب) ثابت ميماند. اين شبکهها از تعداد بسيار زيادي رأس با درجهي بسيار پايين و تعداد بسيار کمي رأس با درجه بالا که به آنها مرکز(Hub) ميگوييم تشکيل شده اند.
- خصوصیت دنياي کوچک شده
بررسي پديدههاي پويا بر روي شبکههاي واقعي نشان ميدهد که ميانبرهايي در تمام اين شبکهها وجود دارد. در واقع پلهاي ارتباطي بين اجزاي مختلف شبکه وجود دارد که بخشهاي مختلف آن را به طور مستقيم به يکديگر وصل ميکند. وجود اين پلها منجر به نزديک شدن اجزاي مختلف شبکه به يکديگر ميشود و بدين وسيله سرعت ارتباطات را افزايش مييابد.
يکي از نشانههاي اين پديده اوّلين بار در شبکههاي آشنايي اجتماعي توسط ميلگرم(Milgram) مشاهده شده است. او در آزمايش مشهور خود از افرادي که به تصادف از ايالت نبراسکا(Nebraska) انتخاب نموده بود، خواست که نامههايي را به فردي در ايالت بوستون(Boston) که تنها نام، شغل و محدودهي زندگي او به صورت تقريبي روشن بود ارسال نمايند. او دريافت که به طور ميانگين هر نامه با 6 بار ارسال به دست فرد مورد نظر رسيده است. اين پديده اخيراً در رد و بدل کردن ايميلها نيز مشاهده شده است.اين خصوصيت در شبکههاي بيولوژيکي و تکنولوژيکي نيز قابل مشاهده است.
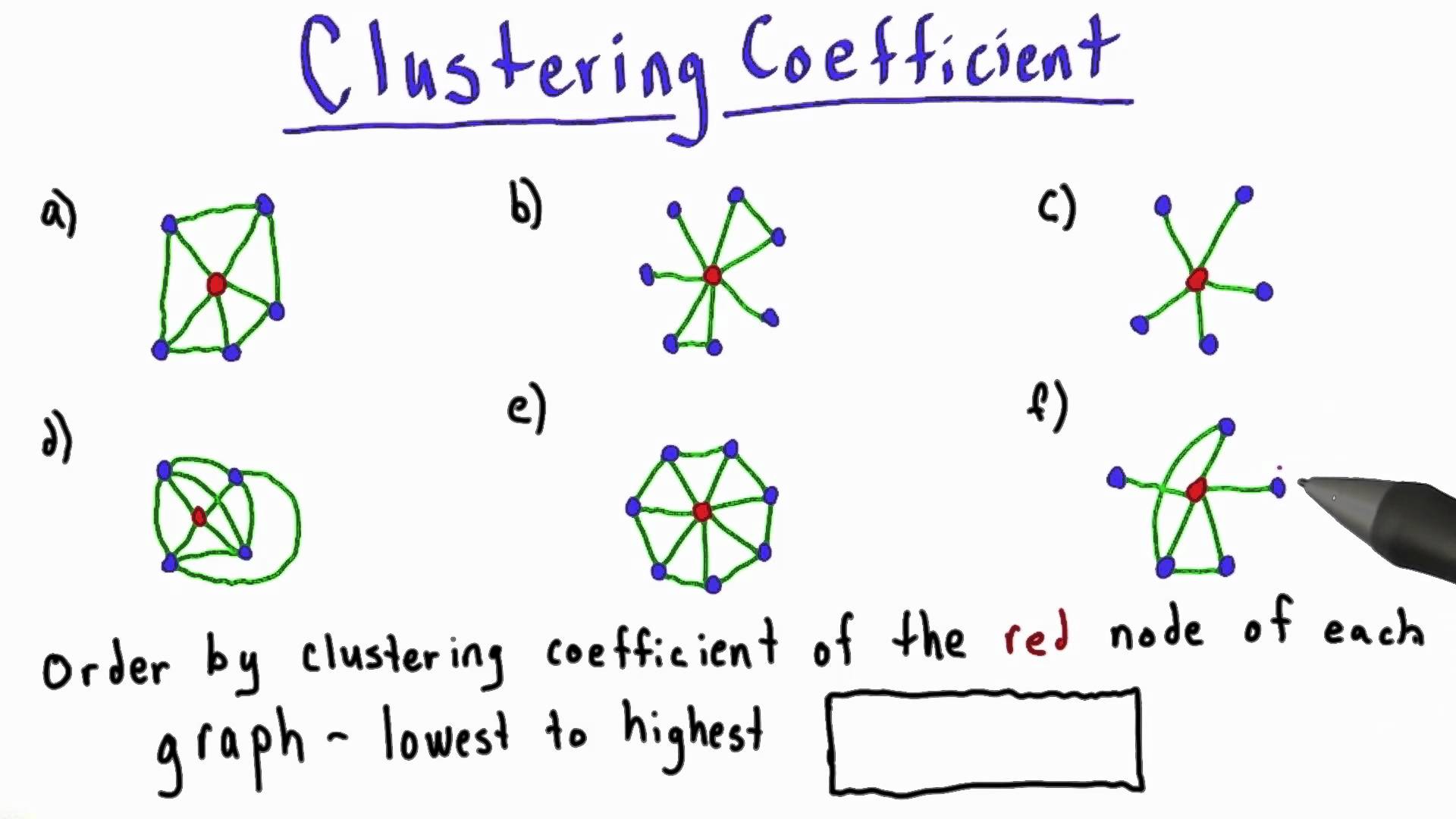
- خصوصیت ضریب خوشه بندی بالا
ویژگی دیگری که در شبکه های اجتماعی یافت میشود دوستی دوستان با یکدیگر است. در صورتی که دو نفر دوست مشترکی داشته باشند احتمال دوست بودن آنها زیاد است و هر چه این دوستان مشترک زیادتر شوند این احتمال نیز بالاتر میرود. درصد افرادی از میان دوستان یک فرد که خود مستقیما با هم دوست هستند ضریب خوشه بندی نام دارد و ویژگی فوق به همین دلیل، ضریب خوشه بندی بالا نامیده میشود. این نام از این جهت به این ویژگی داده شده که خوشه های یک شبکه اجتماعی که در واقع گروههای دوستی را نشان میدهند شامل مجموعه ای از نودها است که ارتباطات میان نودهای این مجموعه دارای چگالی بالایی است. جالب است که خصوصيت دنياي کوچک در تمامي اين شبکه با ضريب خوشهبندي زياد همراه بوده است .
معیار پیمانگی یا ماژولاریتی در سالیان اخیر به عنوان یکی ار اصلیترین معیارهای ارزیابی کیفیت روشهای خوشهبندی مورد استفادده قرار گرفته است. اگر تعداد یالهای درون خوشهای بهتر از حالت گراف تصادفی نباشد، پیمانگی برابر صفر است. حداکثر مقدار پیمانگی زمانی به دست میآید که تمام رئوس هر خوشه به هم متصل باشند و یالی خوشهها را به هم متصل نکند. تجربه نشان میدهد که در گرافهای متعلق به شبکههای اجتماعی این مقدار میان ۰٫۳ تا ۰٫۷ است.
آدرس کانال تلگرام سایت بیگ دیتا:
آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel
جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.
جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.
Visits: 10967
برچسبClustering Coefficient Degree distribute Diameter Rich club Transitivity coefficient بررسی ساختار و توپولوژی گراف شبکه های اجتماعی تحلیل شبکه های اجتماعی توپولوژی گراف شبکه های اجتماعی توزیع فراوانی درجات گره ها خصوصیت استقلال از مقياس دنياي کوچک شده ساختار گراف شبکه های اجتماعی ضریب تراگذری ضریب خوشه بندی ضریب خوشه بندی بالا ضریب کلوپ پولداران فاصله متوسط گره ها قطر گراف گراف کاوی محاسبه کوتاهترین مسیر میان گرههای گراف
همچنین ببینید
بیش ازصد موجودت اسمی برای تشخیص رویداد (Event Detection)
تشخیص رویداد: رصد شبکه های اجتماعی، رویدادهای دنیای واقعی را نشان میدهد و اطلاعات ارزشمندی …
مجموعه داده (dataset) گراف شبکه جاده ای پنسیلوانیا
اطلاعات مجموعه داده (dataset) گراف شبکه جاده پنسیلوانیا یکی از کاربرد های تحلیل شبکه های …
3 دیدگاه
دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.
 خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم
خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم












با سلام و عرض ادب
واقعا موجب احساس خوب برای آدم میشه وقتی مطلبی که تهیه کرده مورد استفاده بقیه قرار میگیره
سلام و وقت بخیر. ممنون بابت مطلب مفیدی که گذاشتین و سایت خوبتون.
ممنون میشم منبع این مطلب را ذکر کنید
سلام وقت بخیر.ممنون از زحمات بی منت شما.
من منابع این مطلبی ک گذاشتین رو لازم دارم
تشکر و سپاس