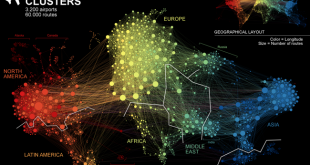
معیار ماژولاریتیmodularity یا پیمانگی با روش Louvain جهت خوشه بندی گراف

• پیمانگی Louvain جهت خوشه بندی:

پیمانگی (modularity) ابتدا به عنوان معیاری جهت تعیین مرحله توقف الگوریتم گیروان و نیومن مورد توجه بود، ولی به سرعت به جزء پر اهمیت تعداد زیادی از الگوریتم‎های تشخیص انجمن تبدیل شد. این معیار فرمولی برای محاسبه کیفیت تقسیم نودها به انجمنهای مختلف ارایه می‌کند که به دلیل ساده و موثر بودن آن به پر کاربردترین معیار کمّی جهت اندازه گیری کیفیت الگوریتم‌های تشخیص انجمن شد. در این بخش به روش‌هایی که از این معیار استفاده می‌کنند توجه می‌کنیم.

معیار پیمانگی در سالیان اخیر به عنوان یکی ار اصلی‌ترین معیارهای ارزیابی کیفیت روش‌های خوشه‌بندی مورد استفادده قرار گرفته است. اگر تعداد یال‌های درون خوشه‌ای بهتر از حالت گراف تصادفی نباشد، پیمانگی برابر صفر است.  حداکثر مقدار پیمانگی زمانی به دست می‌آید که تمام رئوس هر خوشه به هم متصل باشند و  یالی خوشه‌ها را به هم متصل نکند. تجربه نشان می‌دهد که در گراف‌های متعلق به شبکه‌های اجتماعی این مقدار میان 0.3 تا 0.7 است.

• قابلیت های ماژولاریتی

یکی از ویژگی‎های اساسی پیمانگی امکان مقایسه‌ی خوشه‌بندی‌های متفاوت با تعداد خوشه‌های متفاوت است. از آنجایی که لزوما الگوریتم‌های مختلف تعداد خوشه‌های یکسانی را تولید نمی‌کنند، بسیاری از معیار‌های موجود جوابگوی مقایسه‌ی روش‌های مختلف خوشه‌بندی نیستند و امکان استفاده از آن‌ها برای ارزیابی این روش‌ها وجود ندارد. از طرفی، این خصوصیت پیمانگی، این امکان را می‌دهد که بتوان از آن برای تعیین تعداد خوشه‌ها نیز استفاده نمود. بنابراین وقتی که از روش‌های سلسله‌مراتبی بالا به پایین یا پایین به بالا استفاده کنیم می‌توان روند تغییرات پیمانگی هنگام تقسیم یا ترکیب خوشه‌ها را تحت نظر گرفت و خوشه‌بندی که این کمیت را به حداکثر ممکن می‌رساند به عنوان بهترین خوشه‌بندی گراف در نظر گرفت. باید توجه داشته باشیم که بهینه سازی کامل پیمانگی یک مسئله NP-hard  می باشد.

روش Louvain یک الگوریتم ساده و کارا برای یافتن انجمن‌ها در شبکه‌های بزرگ است. این الگوریتم نیز یک الگوریتم حریصانه است که سعی در بیشینه‌سازی معیار پیمانگی در گراف دارد. بر خلاف تمامی دیگر روش‌های خوشه‌بندی، در این روش محدودیت سایز گراف ورودی به محدودیت حافظه ما بستگی دارد، نه به محدودیت زمانی. به همین دلیل، این الگوریتم به راحتی بر گراف‌هایی با صدها میلیون راس و به صورت توزیع شده قابل اعمال است.

این الگوریتم با استفاده از روش‌های حریصانه بر روی ماژولاریتی،  این روش را بهینه کرده و به خوشه‌بندی رأس‌های گراف می‌پردازد.
این بهینه‌سازی در 2 مرحله انجام می‌شود:

• بابهینه‌سازی محلی، این الگوریتم به دنبال گروه‌های کوچک می‌گردد.
• سپس با ادغام گروه‌های کوچک که توانایی ایجاد گروه‌های بزرگ‌تر رادارند خوشه‌بندی را ادامه می‌دهد.

این مراحل را مرتباً تکرار می‌شود تا به مقدار ماکزیمم ماژولاریتی برسیم. همان‌طور که گفته شد، این الگوریتم، یک روش سریع برای پیدا کردن سلسله مراتبی از خوشه‌بندی‌ها در یک گراف بزرگ است.

این الگوریتم شامل دو فاز است که به‌طور متناوب اجرا می‌شوند. فرض کنید که با یک شبکه وزن‌دار با n رأس سروکار داریم. در ابتدا هر رأس را برابر با یک انجمن می‌گیریم. بنابراین در ابتدا به تعداد رئوس، انجمن داریم. سپس برای هر رأس i ، انجمن همسایه j را به نحوی می‌یابیم که به ازای حذف i از انجمن خودش و ملحق کردن آن به انجمن  j، ماژولاریتی بیشینه شود. و سپس رأس i را به انجمن j   اضافه می‌کنیم. این عمل تنها در صورتی انجام می‌شود که میزان ماژولاریتی افزوده شود، در غیر این صورت رأس i در انجمن خودش باقی می‌ماند. این عمل به‌طور مکرر برای تمامی رئوس تکرار می‌گردد تا زمانی که دیگر تغییری اعمال نشود. در این مرحله فاز اول به پایان می‌رسد. باید توجه داشت که در فاز اول ممکن است یک رأس چندین بار میان انجمن‌های مختلف جابجا شود. فاز اول در یک نقطه بهینه محلی متوقف می‌گردد. نقطه‌ای که ماژولاریتی بیشتر با تغییر انجمن هیچ رأسی به دست نمی‌آید. سپس در فاز دوم با ادغام گروه‌های کوچک که توانایی ایجاد گروه‌های بزرگ‌تر را دارند خوشه‌بندی را ادامه می‌دهد.

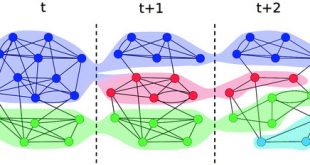
این دو فاز تا جایی تکرار می‌شوند تا تغییری در خوشه‌ها بدست نیاید و پیمانگی به حالت بیشینه برسد. این الگوریتم از خصوصیت خودشبیه بودن گراف های شبکه های اجتماعی استفاده می‌کند. شکل ‏زیر مراحل این الگوریتم را نمایش می‌دهد.

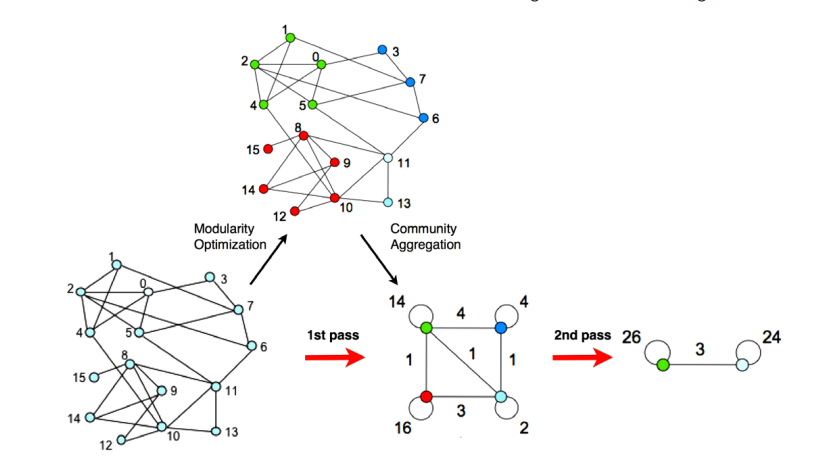
شکل بالا نمایش تصویری مراحل الگوریتم Louvain. هر تکرار از دو فاز تشکیل شده است: فاز اول) بیشینه کردن پیمانگی به طور محلی با جابجایی رئوس در خوشه‌ها. فاز دوم) ساخت خوشه‌های بدست آمده در فاز قبلی و تولید شبکه جدید. دوفاز به طور متناوب تکرار می‌شوند تا جایی که دیگر افزایشی در پیمانگی رخ ندهد.

ویژگی‌های این روش عبارتند از:

• فازهای الگوریتم قابل درک و ساده هستند.
• الگوریتم بسیار سریع است. برای گراف‌های خلوت، الگوریتم مرتبه خطی دارد. دلیل سرعت بالای این روش، ساده بودن محاسبه تفاوت در میزان پیمانگی و  همچنین کاهش سایز گراف بعد از تعداد کمی تکرار است. به نحوی که معمولا بیشتر زمان مصرف شده، در تکرار اول الگوریتم صرف می‌شود.

آدرس کانال تلگرام سایت بیگ دیتا:

t.me/bigdata_channel

آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel

جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.

جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.

Visits: 7360