تئوری گراف به صورت خلاصه (نظریه گراف ها)
عناوين مطالب: '
نظریه گراف ها به صورت خلاصه
در این مبحث به شرح تعاریف اولیه از نظریه گراف (Graph Theory) پرداخته میشود. مطالب این بخش برگرفته از کتاب تئوری گراف نوشته گروس (Gross) میباشد. گراف هر شیء ریاضی شامل یک سری نقاط و اتصالات میان آنها، گراف نامیده میشود. گرافها در طیف وسیعی از مسائل کاربرد دارند. یک گراف میتواند نماینده یک شبکه فیزیکی مثل مدار الکتریکی، شبکه ریلی و یا مدلی از مولکولهای عضوی (Organic Molecules) از بدن باشد. یک اکوسیستم، روابط اجتماعی (Sociological Relationships) ، پایگاهداده و شبکههای اجتماعی را نیز با گرافها نشان میدهند. برای یک گراف تعاریف زیر وجود دارد:
- اگر تمامی اتصالات در یک گراف بدون جهت باشد، به آن گراف بدون جهت (graph) گفته میشود.
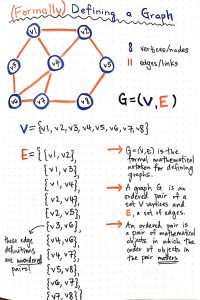
- یک گراف را (G=(V,E با نشان میدهند. عناصر مجموعه V رأس یا گره یا vertex نام دارد. عناصر مجموعه یال E نامیده میشود.
- هر یال شامل مجموعهای از یک یا دو رأس است که نقاط انتهایی (Endpoints) آن نامیده میشوند.
- اگر رأس v نقطه انتهایی یال e باشد، آنگاه v برخورد (Incident) یال e میباشد.
- دو رأس مجاور (Adjacent) همسایه یا مجاور نامیده میشوند.
- گره منزوی یا Isolated Node گره ای هست که با هیچ گره دیگری مجاور نباشد.
- دو یالی که دارای نقطه انتهایی مشترک میباشند، همسایه یکدیگر خوانده میشوند.
- یالی که دارای نقاط انتهایی یکسانی است را حلقه (Self-loop) مینامند.
گراف ساده: اکثر تئوریهای نظریه گراف برای گراف ساده (Simple Graph) بیان شده است. علت این موضوع این است که خیلی از مسائل گرافهای عمومی را میتوان به یک گراف ساده کاهش داد. بنابراین تعاریف زیر را داریم:
- گراف ساده، گرافی است که دارای حلقه نبوده و مابین تمامی رأسهای آن حداکثر یک یال وجود داشته باشد.
- گراف بیاهمیت (Trivial Graph): گرافی است که تنها از یک رأس و هیچ یالی تشکیل شده است.
- گراف پوچ(Null Graph): گرافی است که هیچ یال و گرهای نداشته باشد.
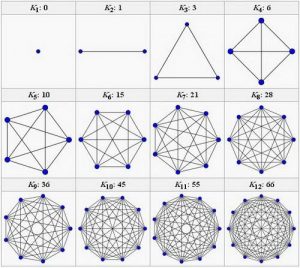
گراف کامل : گرافی که بین تمام راس ها دقیقا یک یال وجود داشته باشد.
Cycle: گرافی که هر راس به همسایه قبلی و بعدی متصل است.(شبیه linkedlist)
Wheel: گرافی که به cycle یک راس اضافه میکند و آن راس را به تمام رئوس دیگر متصل میکند .
گراف چندگانه: اگر میان دو گره بیش از یک یال وجود داشته باشد، به این یالها، یالهای چندگانه گفته میشود. اگر یک گراف دارای یالهای چندگانه باشد، به آن گراف چندگانه میگویند.
گراف جهتدار: گرافهایی که در آنها تمامی یالها دارای جهت میباشند را گراف جهتدار(Digraph) مینامند. برای گراف جهتدار تعاریف در ادامه وجود دارد:
- یال جهتدار یا پیکان(Arc)، یالی است که یکی از نقاط انتهایی آن دم (Tail) و انتهای دیگر سر نامیده میشود.
- گراف ساده جهتدار گرافی است که هیچ یال حلقهای نداشته و مابین تمامی رأسهای آن حداکثر یک یال جهتدار وجود داشته باشد.
گراف مخلوط Mixed Graph: گرافی است که در آن برخی لبه ها جهت دار و برخی بدون جهت است.
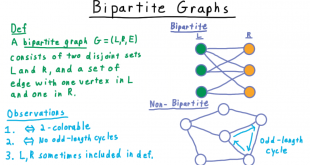
گراف دوبخشی: اگر بتوان تمامی گرههای موجود در گراف را به دو دسته تقسیمبندی نمود، به طوری که یک نقطه پایانی یالها در یک دسته و نقطه پایانی دیگر در دسته دیگر قرار گیرد، به آن گراف دو بخشی (Bipartite Graph) گفته میشود.
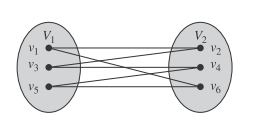

روش تشخیص گراف دوبخشی
برای تست این شرط و افراز به دو مجموعه، میتوانیم از هر دو الگوریتم جستوجوی عمقاول و جستوجوی سطحاول استفاده کنیم. کافیست نحوه علامت گذاری مزاعفی در این دو الگوریتم را به گونه ای اضافه کنیم که از رأسهای با رنگ ۰ به رأسهای با رنگ ۱ برویم و برعکس. حال اگر به رأسی با علامت ۱ رسیدیم که همسایهای از آن از قبل رنگ ۱ را داشت، پس در نتیجه دور فرد پیدا شده است و نمیتوان این کار را کرد؛ برای علامت ۰ نیز به همین ترتیب است. حال اگر هیچ یک از این دو حالت اتفاق نیافتد، در نتیجه میتوان این کار را کرد و رأسهایی که علامت ۱ را دارند در یک دسته و بقیه را در دسته مقابل قرار میدهیم.
دقت کنید که ممکن است گراف ناهمبند باشد در نتیجه برای تمام رأسهای دیده نشده این الگوریتم را تکرار میکنیم.
پیچیدگی الگوریتم
از آنجا که از الگوریتم های پیمایش استفاده میکنیم، مرتبه زمانی برابر مرتبه زمانی جستوجو ها است که برابر (O(n+e است. n تعداد رأسها و e تعداد یالها است.
درجه: از خصیصههای مهم در نظریه گراف، درجه Degree گراف میباشد. درجه گرهی vi در گراف را با (Deg(vi نشان داده، و برابر با تعداد یالهای است که یکی از نقاط انتهایی آنها گرهی vi بوده به اضافه دو برابر تعداد یالهای حلقه به همان رأس میباشد.
- دنباله درجه یک گراف، شامل دنباله درجههای گراف به صورت صعودی میباشد.
- درجه داخلی (Indegree) یک گره در گراف جهتدار عبارت است از تعداد پیکانهایی که به سمت آن گره اشاره میکنند.
- درجه خارجی (Outdegree) یک گره عبارت است از تعداد پیکانهایی که از آن گره خارج میشوند. یالهای از نوع طوقه شامل یک درجه داخلی و یک درجه خارجی میباشند.
- رأس منزوی (Isolated) رأسی است که دارای درجه صفر باشد.
گام: گام w در گراف G دنبالهای از یالها و گرهها میباشد.
- در یک گام اگر یالها دارای جهت باشند، به آن گام جهتدار میگویند.
- طول یک گام برابر با تعداد یالهای آن است (یالهای تکراری نیز شمارش میشوند)
- اگر در یک گام، گرهی آغازی و پایانی یکی باشند، به آن گام بسته (Closed Walk) گفته میشود.
دنباله: یک دنباله (Trail) در گراف، گامی است که هیچ یالی بیشتر از یک بار در آن مشاهده نشود.
- اگر در یک دنباله، تمامی یالهای یک گراف برای یک بار پیمایش شود، به آن دنباله اویلری (Eulerian Trail) میگویند.
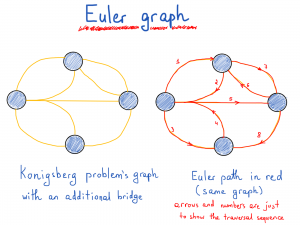
مسیر: یک مسیر در یک گراف، دنبالهای است که در آن هیچ گرهای بیشتر از یک بار مشاهده نشود.
- اگر گرهی ابتدایی و انتهایی در یک مسیر یکسان باشد به آن مدار یا دور گفته میشود.
- یک گره ایزوله، یک گام، دنباله و مسیر بیاهمیت میباشد.
سیکل یا دور: یعنی اینکه پیمایش گراف را از یک راس شروع کنیم و به همان راس برگردیم. گرافی که سیکل ندارد را جنگل گویند و اگر همبند باشد این گراف درخت است.
گراف همبند یا connected و گراف ناهمبند: گرافی که بین دو راس آن حداقل یک مسیر وجود داشته باشد.
مولفه: گرافی که ناهمبند است هر قسمت از گراف یک مولفه است.
گراف ترانهاده یا Gt: گراف جهت داری است که جهت یال های آن برعکس شده باشد. یکی از استفاده های گراف ترانهاده در پیدا کردن مولفه های متصل قوی است.
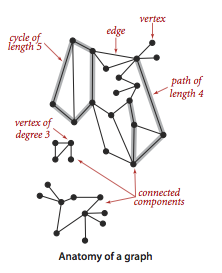
فاصله و اتصال: فاصله میان دو گره در یک گراف، طول کوتاهترین گام Geodestic میان آن دو است.
- در گراف جهتدار، فاصله میان دو گره برابر با طول کوتاهترین گام جهتدار میان آنهاست.
- گراف را متصل یا همبند (Connected) مینامند، اگر میان هر دو گرهای یک گام وجود داشته باشد.
- گراف جهتدار را به طور ضعیف همبند (Weakly Connected) است، اگر گراف بدون جهت متناظر با آن متصل باشد.
- گراف جهتدار قویاً همبند (Srtongly Connected) میباشد اگر میان هر دو گرهای در آن، حداقل یک گام جهتدار وجود داشته باشد.
- گریز از مرکز (Eccentricity) یک گره در گراف همبند برابر با فاصله دورترین گره نسبت به آن در گراف میباشد.
- شعاع (Radius) یک گراف همبند برابر با طول کمترین مقدار گریز از مرکز آن است.
- قطر (Diameter) یک گراف همبند، برابر با بزرگترین مقدار گریز از مرکز آن است.
روش محاسبه قطر گراف
توجه کنید که قطر همیشه برابر طولانیترین مسیر نیست، برای مثال در گراف متشکل از یک دور، طولانیترین مسیر برابر n−1 است، ولی قطر n/2 است.
-
گرافهای بدونجهت و بیوزن که با n بار جستوجوی سطحاول قابل حل است.
- گرافهای وزندار که راهحلهای مختلفی از جمله (O(n³دارد. مثل الگوریتم فلوید-وارشال و الگوریتم دایکسترا .
همریختی ایزومورفیک: دو گراف همریخت (Isomorphism) یکدیگر میباشند اگر از لحاظ ساختاری (Structrual) شبیه به هم باشند؛ به طوری که تناظر یک به یک میان یالها و گرههای آن دو بر قرار باشد.
زیرگراف: زیرگراف (Subgraph) گراف G را H مینامند.
- گراف همریخت گراف G را میتوان یک زیرگراف آن در نظر گرفت.
- موءلفه (Component) گراف، بزرگترین زیرگراف متصل آن میباشد.
انواع نمایش گراف
گراف را به صورت های مختلفی میتوان نشان داد روش های زیر معروفترین آنها است. برای درک بهتر به مطلب ساختمان داده منطقی گراف مراجعه کنید.
- ماتریس مجاورت
- ماتریس برخورد
ماتریس مجاورت
ماتریس مجاورت، ماتریسی است که حاوی اطلاعات مربوط به تعداد یالهایی بین رأسهای مختلف گراف است. محتوای این ماتریس صفر و یک است. اگر راسی به راس دیگری یالی داشته باشد محتوا یک میشود در غیر این صورت صفر. ماتریس مجاورت در زیر میبینید.
- دو گراف همریخت دارای ماتریس مجاورت یکسانی هستند.
برای بهتر متوجه شدن این ماتریس، سطر و ستون های ماتریس مجاورت هر دو شامل نام راس های ما هستند.به صورت زیر:
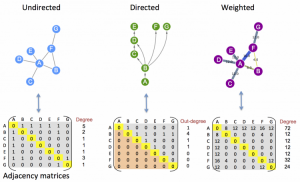
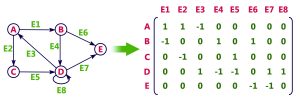
ماتریس برخورد
نحوه محتوا در ماتریس برخورد مشابه ماتریس مجاورت است.(همان صفر و یک)در ماتریس برخورد، سطرها نام راس ها و ستون ها نام یال ها است. تصویر به سادگی این قضیه را بیان میکند. ماتریس برخورد هر ستون که دو عدد یک داشته باشد یعنی یالی که در آن ستون است بین دو راس مشخص قرار دارد. اگر در یک ستون فقط یک عدد یک باشد نشان دهنده طوقه (یال به خود) در آن راس است.
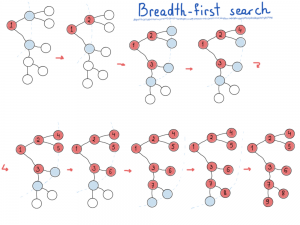
پیمایش گراف
پیمایش گراف (Graph traversal) در حالت کلی به معنی گذشتن و دیدن تمام راسهای گراف است و معمولا پیمایش از طریق یالهای موجود در گراف انجام میشود. معمولا پیمایش گراف به تنهایی ارزش خاصی ندارد و هدف از پیمایش، محاسبه یا پیدا کردن چیز دیگری است. برای مثال شاید با نگاه کردن به یک گراف بتوانید خواص آن را پیدا کنید و مسئله را حل کنید؛ اما در کامپیوتر به دلیل محدودیتهابه همین راحتی نمیتوان این کار را کرد. الگوریتمهای پیمایش در حرکت روی گراف و پیدا کردن خواص آن به ما کمک میکنند.
اول سطح
اول عمق
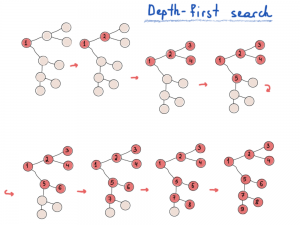
رنگ آمیزی یا علامت گذاری
در درختها و گرافهای بیدور معمولا این مشکل وجود ندارد، چراکه مسیر تکراری نداریم و نیازی به چک کردن رأس یا یال تکراری نیست.
هنگامی که گراف دور دارد، برای جلوگیری از رفتن مسیرهای تکراری و نیافتادن در دام دور، نیاز به علامتگذاری و رنگ کردن رأسها یا یالها داریم. بنابراین هرگاه وارد رأس یا یالی شدیم آن را علامت میزنیم تا دفعه بعدی که وارد آن شدیم بتوانیم بفهمیم که قبلا هم اینجا بودهایم یا نه؛ سپس با توجه به این نکته میتوانیم بفهمیم که ادامه پیمایش از این رأس یا یال را ادامه دهیم یا آن را همین گونه رها کنیم.
معمولا در بدنهی الگوریتمها از این مطلب به اسم رأس دیده شده (visited) یا علامت زده شده (marked) یاد میشود و لیست یا آرایهای برای نگهداری علامتها اختصاص میدهند.
کاربردهای الگوریتم جستجوی اول عمق
الگوریتم DFS و روش پیمایش آن کاربردهای فراوانی دارد که در ادامه به چند مورد مهم اشاره میشود.
1– تشخیص وجود مسیر: با استفاده از الگوریتم dfs میتوان وجود مسیر از گره مبدأ به گره دیگر را بررسی کرد.
نکته: اگر گراف همبند و بدون جهت باشد همواره مسیر بین هر دو گره دلخواه وجود دارد و نیاز به استفاده از این الگوریتم نیست. تذکر: در الگوریتم BFS اگر گراف بدون وزن باشد، مسیر مشخص شده توسط الگوریتم به طور حتم کوتاهترین مسیر از گره مبدأ به مقصد است؛ اما در مورد الگوریتم DFS این خاصیت لزوما برقرار نیست.
2– تولید درخت پوشا: درخت پوشا یعنی همه نود های گراف روئیت شوند. خروجی الگوریتم DFS روی یک گراف بدون جهت و همبند یک درخت پوشا است. در مورد گرافهای جهتدار ممکن است متناسب با گره مبدأ چنین درختی ساخته شود یا نشود.
3– تشخیص دور در گراف: اگر در حین پیمایش گراف، یکی از گزینههای پیمایش گرهی باشد که قبلا پیمایش شده است، به معنی وجود دور در گراف است.
نکته: اگر در یک گراف بدون جهت بیش از|V|−1 یال وجود داشته باشد، گراف به طور حتم دور دارد (چرا؟).
4– تشخیص دو بخشی بودن گراف: یک گراف دوبخشی است اگر و فقط اگر بتوان گرههای آن را با استفاده از دو رنگ به نحوی نشانهگذاری کرد که هیچ دو گره مجاوری همرنگ نباشند. برای تشخیص دوبخشی بودن گراف با استفاده از الگوریتم DFS، هر گره در پیمایش با رنگ مخالف گره پیشین نشانهگذاری شده و بررسی میگردد که آیا از گرههای پیمایششدهی مجاورش گرهی با همین رنگ نشانهگذاری شده است یا نه. اگر چنین گرهی یافت شود به معنی عدم امکان رنگ شدن گراف با دو رنگ و در نتیجه دو بخشی نبودن گراف است. یافت نشدن چنین گرهی در هر مرحله تا انتهای اجرای الگوریتم به معنی دو بخشی بودن آن است که این دو بخش توسط رنگها متمایز شدهاند.
5– حل مارپیجهای تکمسیر: الگوریتم BFS راهکاری است که در یافتن کوتاهترین مسیر در مسیرهای مارپیچ (Maze) کاربرد دارد. اگر مسیر رسیدن به هر نقطه از مارپیچ یکی باشد (دوری در مارپیچ نباشد یا گراف معادل مارپیچ یک درخت باشد) میتوان از الگوریتم DFS نیز استفاده کرد. چرا که در چنین حالتی تنها یک مسیر به مقصد وجود داشته و کوتاه بودن آن مطرح نیست.
6- تشخیص اینکه گراف هم بند است یا خیر: و اگر نا همبند است، چند مولفه دارد. اگر همه رئوس گراف با یک فراخوانی تابع DFS-VISIT ملاقات شوند همبند است و در غیر این صورت به تعداد فراخوانی های این تابع مولفه دارد.
7- یافتن ترتیب توپولوژیک: یعنی هر راسی که ملاقات میشود یا درجه ورودی اش صفر باشد یا اگر صفر نیست رئوس وارد شده قبلا ملاقات شده باشند. فقط گراف بدون سیکل جهت دار یا dag دارای ترتیب توپولوزیک است.
8- یافتن مولفه های متصل قوی در گراف جهت دار
9- یافتن نقاط انفصال یا راس برشی در پراف غیر جهت دار:
10- یافتن پل: پل یالی است که اگر حذ شود تعداد مولفه های گراف بیشتر می شوند. در واقع پل یالی است که عضو هیچ سیکلی نباشد که به کمک کمک پیمایش اول عمق میتوان پلها را پیدا کرد.
مرتبه زمانی یک الگوریتم
برای تخمین زمان اجرای الگوریتم و میزان پیچیدگی آن، از نمادهایی به نام نمادهای مجانبی (حدی) استفاده میشود. این نمادها عباتند از: O ، Ω، Θ و o، ω که هر کدام طبق روش خاصی محاسبه میشوند و در تحلیل الگوریتم کاربرد فراوانی دارند.
رشد توابع
گوییم رشد تابع f(n) از تابع g(n) بیشتر است اگر n به بینهایت میل کند () آنگاه f(n) زودتر به ∞ میل میکند. ترتیب رشد زیر برای توابع نام برده قابل اثبات است:
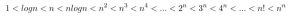
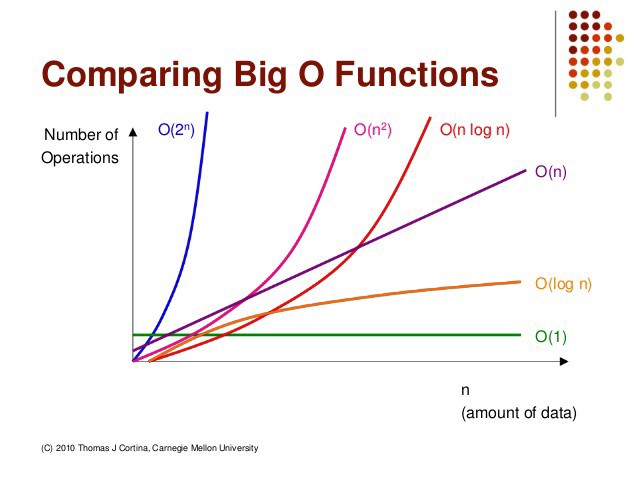
1 یعنی بدون رشد، یعنی به n وابسته نیست. مثلا حلقه ای که 1000 بار اجرا میشود رشدش 1 است.
- اگر جواب حد برابر صفر باشد، نتیجه میگیریم، رشد f از g کمتر است.
- اگر جواب برابر ∞ باشد، رشد f از g بیشتر است.
- اگر برابر k ≠ 0 باشد، f و g رشد یکسان دارند.
وقتی اندازه ورودی (n) بزرگ باشد، بیان دقیق زمان اجرا برحسب n ضروری نیست زیرا جمله با بزرگترین درجه در زمان موثر است. مثلا اگر زمان اجرای الگوریتمی باشدف به ازای nهای بزرگ فقط مهم است. میتوان با نمادهای مجانبی این تفسیر را بهتر نشان داد. در بیان نمادها فرض میشود که دامنه اعداد طبیعی N={0, 1, 2, …} است.
نمادهای مجانبی:
O : کران بالای مجانبی
Ω : کران پایین مجانبی
θ : کران دوطرف مجانبی
نماد O بزرگ
در نظریهٔ پیچیدگی محاسباتی، نماد O بزرگ (به انگلیسی: Big O notation) برای نشان دادن رابطه میان تعداد دادهها و منابع محاسباتی مورد نیاز برای حل یک مسأله با استفاده از یک الگوریتم استفاده میشود. استفاده از این نماد معمولاً برای بررسی زمان و یا حافظه مورد نیاز برای حل مسألهای با تعداد زیادی ورودی میباشد.
در ریاضیات علامت O بزرگ رفتار حدی یک تابع را وقتی آرگومانهای آن به یک عدد خاص یا به بینهایت میل میکند، توصیف میکند. علامت O بزرگ به کاربر اجازه میدهد که تابع را ساده کند تا بر روی نرخ رشد آن متمرکز شود؛ بنابراین توابع مختلف با نرخ رشد یکسان میتوانند دارای یک علامت O مشابه باشند.
هرچند این علامت به عنوان بخشی از ریاضیات محض گسترش یافت ولی هم اکنون در تئوریهای پیچیدگی محاسبات هم بارها استفاده میشود. بدترین حالت یا حالت میانگین زمان اجرا یا حافظه مورد استفاده یک الگوریتم اغلب به صورت تابعی از طول داده ورودی با استفاده از علامت O بزرگ توصیف میشود.
این به طراحان الگوریتم اجازه میدهد که رفتار الگوریتمهایشان را پیشبینی کنند و تصمیم بگیرند که کدام الگوریتم را استفاده کنند (بدون توجه به معماری رایانه یا میزان آهنگ ساعت آن).
برخلاف O نماد Θ که یک تابع را از بالا و پایین بصورت مجانبی (حدی) محدود می کند، نماد O یک کران بالای حدی مشخص میکند. وقتی تابعی را با استفاده از علامت O بزرگ توصیف میکنیم بطور معمول تنها یک کران بالا برای نرخ رشد آن تابع فراهم میکنیم.
بنابراین O یک کران بالا برای تابع مشخص میکند. ما مینویسیم f(n)=O(g(n)) اگر f(n) عضوی از O(g(n)) باشد.
نکته : وقتی گفته میشود زمان اجرای الگوریتم O(n2) است یعنی الگوریتم هر جوری اجرا شود، مرتبه ی زمانی اجرای آن یا n2 است و یا از n2 کمتر است.
نماد امگا Ω
نماد Ω یک کران پایین حدی برای تابع مشخص میکند
نماد تتا Θ
تتا(جی(ان)) برابر است با اف(ان) به طوری که وجود دارد سی1، سی2 و ان0ی بزرگتر از 0 که به ازای هر ان بزرگتر مساوی ‘ان0’ داریم: 0 کوچکتر مساوی سی1 جی(ان) کوچکتر مساوی اف(ان) کوچکتر مساوی سی2 جی(ان)
میرانی سختی P و NP و NP-Complete و NP-Hard به زبان ساده
کلاس P
هر مسئلهای که بتوان در زمان چندجملهای حل کرد، به کلاس P تعلق دارد. پس مرتبسازی سریع مسئلهایست در کلاس P چون زمانش حداکثر مربعی است. مثل مسائل ماتریس
کلاس NP
مسایلی که خودش شاید در زمان چندجملهای حل نشود، ولی اگر یک راهحلش را داشته باشیم، میتوانیم درستی آنرا در زمان چندجملهای وارسی کنیم، NP است. پس مسئله یافتن یک تور کمینه بین چند شهر NP است. علتش اینست که اگرچه خودش در زمان نمایی حل میشود ولی اگر یک تور داشته باشیم میتوانیم در زمان مثلا مربعی وارسی کنیم که درست است. پس مرتبسازی سریع هم علاوه بر کلاس P، در کلاس NP هم هست: هم خودش در زمان مربعی حل میشود، هم راهحلش در زمان مربعی وارسی میشود.
کلاس NP-Complete
میبینیم که دو دسته مسائل در کلاس NP هست که یکی سختتر از دیگری است. دسته سختتر را مسائل NP-Complete میگویند. یعنی پیدا کردن تور بهینه NP-Complete است ولی مرتبسازی سریع فقط NP است و نیز P. مثل ایزو مورف گرفتن از کل جامعه آماری
کلاس Np-Hard
NP Non-deterministic Polynomial-time hard)→NP-hard)
سپس محققان مسائل حتی خیلی سختتری را هم پیدا کردند. اینها مسائلی هستند که نه تنها خودشان در چندجملهای حل نمیشوند، بلکه راهحلشان هم شاید در چندجملهای قابل وارسی نباشد. به این مسایل NP-Hard میگویند. مسایل NP-Complete، اِنپی سخت هم هستند ولی مسایلی در NP-Hard هست که سختتر از بقیه است و NP-Complete نیست. سختی یعنی خیییلی طول میکشد که مسئله حل شود. راهحل را میدانیم، ولی انبوهی از حالتهای مختلف را باید بررسی کنیم تا به جواب برسیم.
مسائل NP-Hard خانوادهایست از چندهزار مسئله با کاربردهای روزمره و واقعی. مثلا پیدا کردن کمترین میزان سیمکشی و اتصالات در یک مدار الکترونیک. اما بخاطر سختی حل آنها از روشهای دیگری استفاده میشود. یکی از اینها الگوریتمهای تقریبی هستند. دوم الگوریتمهای ابتکاری و تصادفی هستند. همه این روشها یک مسئله NP-Hard را دقیق حل نمیکنند، ولی مزیتشان اینست که جواب تقریبی نزدیک به دقیق را خیلی زود و تند برای ما تولید میکنند.

منبع:
عمده مطالب این بخش اقتباسی از پایاننامه کارشناسی ارشد آقای احسان شرکت در دانشگاه تهران میباشد.
دانشنامهی المپیاد کامپیوتر ایران
http://opedia.ir
http://notif.ir/asymptotic-notations-in-algorithm-design-2386.html.
 Loading...
Loading...
اسلاید های کلاس و کارگاه تحلیل شبکه های اجتماعی و تئوری گراف
آدرس کانال تلگرام سایت بیگ دیتا:
آدرس کانال سروش ما:
https://sapp.ir/bigdata_channel
جهت دیدن سرفصل های دوره های آموزشی بر روی اینجا کلیک کنید.
جهت ثبت نام در دوره های آموزشی بر روی اینجا کلیک کنید.
Visits: 34651
برچسببه صورت خلاصه پیمایش گراف تئوری گراف تئوری گراف به صورت خلاصه درجه رنگ آمیزی گراف زیرگراف گام گراف جهتدار گراف چندگانه گراف ساده ماتریس برخورد ماتریس مجاورت مسیر نظریه گراف
همچنین ببینید
تشخیص موتیف یا زیر گراف های پرتکرار با برنامه Cytoscape
معرفی موتیف در مطالب قبلی به آموزش Cytoscape پرداختیم در آموزش امروز به نحوه تشخیص …
مدل داده و ساختارهای منطقی ذخیره سازی گراف
با یکی دیگر از مباحث مبانی در حوزه گراف کاوی و تحلیل شبکه های اجتماعی …
3 دیدگاه
دیدگاهتان را بنویسید
برای نوشتن دیدگاه باید وارد بشوید.
 خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم
خانه بیگ دیتا تحلیل شبکه های اجتماعی، متن کاوی، داده کاوی، اوسینت و داده های حجیم













سلام بسیار مطالب عالی است در مورد ارتباط مغز و شبکه ها لطفا مطلب بفرستید .
ممنونم – خیلی خوب و تر تمیز مطالب رو یکجا جمع کرده بودید.